A common question when purchasing a
telescope is
what "power" it is. The power of the
telescope is
the ability to magnify an object.While
magnification is really not as important as field of
view of aperture, to determine the power of a
telescope, simply divide the eyepiece diameter to
the
telescope focal length:
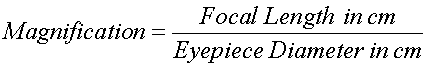
Eyepiece diameter is also known as the eyepiece focal length. Do not confuse this with the exit pupil which is a different concept: based on the telescope aperture and magnification or telescope focal and telescope focal ratio. The exit pupil is the term that defines the size of the light cone that enters your eye.
Additionally, the resolution of a
telescope must be
considered. For ideal "seeing" conditions, the
following formula applies:
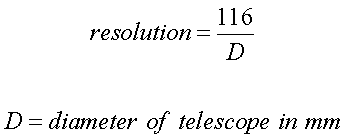
Example: a 254mm
telescope (a 10")
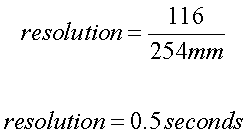
The size of an image depends on the focal length of
your
telescope. For example, the longer the focal
length, the larger the object:
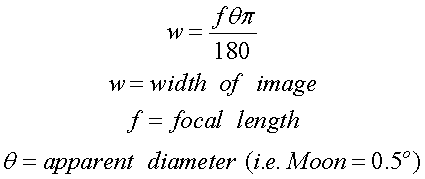
How faint an object can your
telescope see:
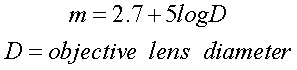
Where m is the limiting
magnitude. Example, our 10"
telescope:
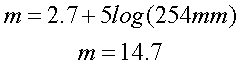
The faintest object a 10"
telescope can see is with
a visual
magnitude of 14.7 (Pluto has a
magnitude of
around 13.8).
Back to Top
|

