Calculus is a style of
mathematic invented by Sir
Isaac Newton. The word "calculus" which means rock.
Interesting choice of names as Calculus is assumed
to me one of the harder sub-topics that make up the
subject of
mathematics.My Calculus teacher used
to tell us that calculus really isn't that hard, all
you have to imagine is that calculus is focused more
narrowly on a particular equation than a simple a +
b = c.
An example he used was a car traveling to the
local store. You may have traveled at a top speed of
30 km/h, but you did not travel at that velocity the
entire distance. Calculus is used to take into
account stops and starts, twists and turns in the
road, time it take entering and exiting the vehicle
- things like that that will result in a much more
realistic equation.
My
mathematics is a bit rusty, so if there are
errors please let me know.
I like to think of Calculus as three individual
topics:
Limits
Derivatives
Integrals
One of the common terms found in this subject is the
function:
f(x)
A function is a relation that
uniquely describes a set of numbers and associated
it with a set of variables. For example:
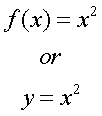
Limits:
A limit describes a function up to a point.
Recall that graphic plots in
Algebra are lines that
continue on. A limit is a tool that limits (as the
name suggests) the duration of a plotted set of
values.
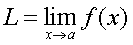
where x is the value of the function
and a = the value of the limit.
Back to Top
Derivatives:
A derivative is a rate of change of some example
- the the car traveling to the corner store. Its is
basic form, a derivative is:
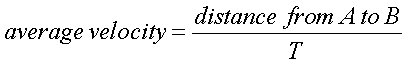

Where A is the house, B is the corner store and T
is the total time from A to B.
Now if you want to know how fast you were
traveling from a specific part of the trip, the
power of the derivative comes through. First you
need to splice up your line:

And pick two point - X and Y. Using the term:
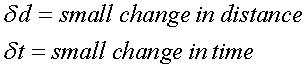
To get:
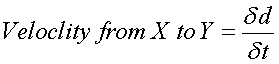
Insert a limit to determine
instantaneous velocity:
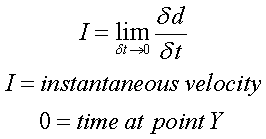
Now for the biggie: for the
derivative of the distance with respect to time,
insert limits and functions to assess all the points
on the line:
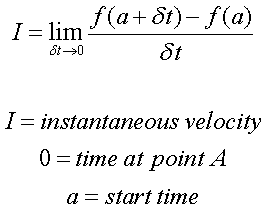
Back to Top
Integrals:
An integral is a term used to define the sum
total of all parts. However, the integral is used to
find unknown small bits from a know larger size. To
do this, we need to use a differential equation:
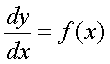
dy and dx are "some
number," that is we don't know the value yet. If we
choose to solve for y, the equation takes form:
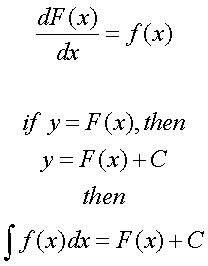
Where C is a known value.
This may seem a bit confusing, but to use an
example:
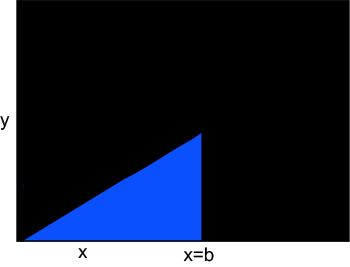
You want to know the area of the
blue triangle. By using an integral, you can. First
we assign the function:
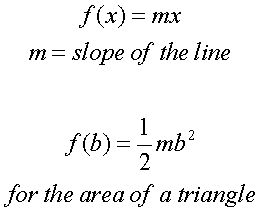
For the integral function from 0 to
x=b:
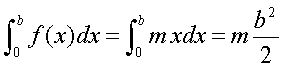
Back to Top
|

