|
|
|
 |
|
| Our Sun - Advance Topics |
| |
This section will contain advanced topics
regarding the Sun. If you have material to present,
please contact us.
|
|
 |
|
To view the advanced topics, please click the link
of interest: Energy Transport
(Link to) Fusion - Coming Soon
(Link to) Evolution of the Solar System - Coming
Soon
(Link to) Helioseismology - Coming Soon
There are five methods of
energy transport,
and they all work together: radiation,
opacity,
convection,
mixing, and
rotation.
Radiation:
The photon released by nuclear
fusion begins its trip to the surface by way of the
random walk. The photon must pass through existing
molecules, so it goes into a process of
re-absorption and re-emission - mostly because of
the very high energy of the photon (Wien's Law). In
order to determine the distance traveled by every
interaction, we measure the "mean free path" of the
photon. The distance between interactions is equal
to the energy of the photon and the square root of
its interactions. |
|
 |
|
This means the overall displacement (d) will only be
high if there are a very large number of
interactions. This can take a long time - somewhere
along the lines of 10,000,000 years and 2 x 1022
collisions for one photon. The final result of this
radiation is a few high energy photons will turn
into a larger group of lower energy photons.
Back to Top
Opacity:
We all know what opacity is, but what this means
for stellar physics is the resistive properties of
opacity. |
|
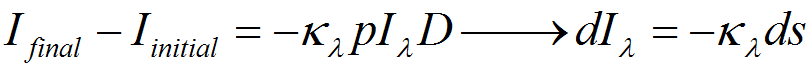 |
|
This looks worse than it is. What we are trying to
determine is with a given intensity, how does
opacity affect the final result. An analogy: We
have an open ended tube filled with a density (p) or
a material (D) that has a certain mass with an
opacity (k) that is called an "absorption
coefficient" - which is a known number depending on
the material. A photon with a level of intensity (I
initial) enters the tube and is resisted by the
material in the tube and exists with an altered
(less) intensity (I final).
The mechanism of opacity varies, but is based on
one of four parameters:
| bound-bound absorption |
an atom with a free orbit of a
particular energy level absorbs a photon of
equal energy to occupy the gap |
| bound-free absorption |
an atom with a populated orbit of a
particular energy level is met with a photon
with a higher energy level and bumps the
electron out of orbit by transferring the
energy difference |
| free-free absorption |
an electron absorbs the energy of a
nearby photon and moves up in energy level |
| scattering |
high energy photons can knock an
electron out of orbit and does not occupy
the gap - both are free |
The "mean-free" path when opacity is part of the
equation: |
|
 |
|
A more complicated version is called the Rosseland
mean opacity - this is an average of all wavelengths
to determine the sum of all the opacity for a given
opacity (based on temperature, density, and
composition) |
|
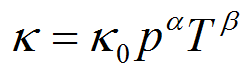 |
|
There is much more detail in regards to opacity, but
what all of this shows is that increased opacity
generally decreased temperature and reduces the
energy level of photons. Back to
Top
Convection:
This is a pretty simple idea because we witness
the effects of this on Earth. Hot, less dense air
rises while cold, more dense air falls. This is
called convection. So can astrophysicists confuse
this simple idea? Yes: |
|
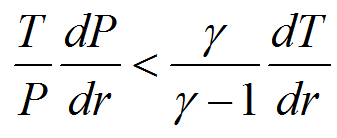 |
|
Kidding aside, this is actually an easy equation to
understand. This is called the condition of
convection, and shows what is required: temperature
(T), pressure (P), radius (r), and specific heat of
the object in question (γ).
The value 'd' is just some number - i.e. 'dP' is the
value assigned to P. Back to Top
Mixing:
The idea of mixing
is still new to stellar astrophysics, but basically
it is the result of pressure and movement of heavier
material outside the realm of radiation or
convection. This of adding sugar to tea - you are
not altering the composition (or even the
temperature) of the tea, you are only mixing the
sugar with the tea. However, it is this end result
that can be applied to the opacity dynamics.
Back to Top
Rotation:
Mixing and rotation
provide the same interactions of material within the
convective layers, but rotation also provides the
engine needed for sunspot formation. This is a
process of energy transport as the sunspot magnetic
field reconnection allows for the liberation of some
excess material near the surface of the Sun.
Back to Top
Fusion
The Solar Nebula
Helioseismology
Back to Top |
|
|

