Just like any other subject in math, Geometry is
loaded with a wide variety of subtopics - including
the ubiquitous Trigonometry. Just as the previous
pages however, we will focus on the basics - again
to help stir the memory a bit.The basic form of
Geometry - that is lines, perimeters, areas - is
called Euclidean Geometry named after its Greek
inventor, Euclid. Another name for Euclidean
Geometry is Plane Geometry.
The section will only cover:
Perimeter, Area, and Volume
Angles
Basic
Trigonometric Functions
Perimeter, Area, and Volume:
A perimeter is the length around the outside of
any geometric shape. Simply add the lengths of the
sides together.
Area is the measure of space inside any
two-dimensional geometric shape.
Volume is the measure of space inside any
three-dimensional geometric shape.
Area of a triangle:
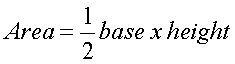
Area of a rectangle and parallelogram:
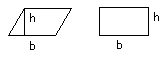
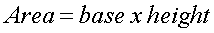
The Circle:
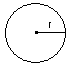
The circumference of a circle is the same as the
perimeter of a triangle or rectangle. To find the
circumference:
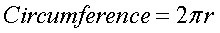
r = radius of a circle
π = pi
= 3.14
The
area of a circle:
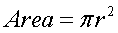
Three dimensional objects:
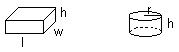
Area of the rectangle solid:
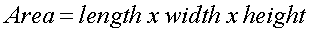
Angle of the cylinder:
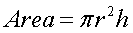
Area of a Sphere:
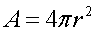
Volume of a Sphere:
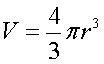
Back
to Top
Angles:
Complimentary Angles:
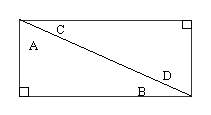 |
Two angles are complimentary when the
sum of their angles is 90o. In
the image on the left, angles A and B are
complimentary and angles A and C are also
complimentary. |
|
 |
|
The remaining angle
definitions will use the image above. |
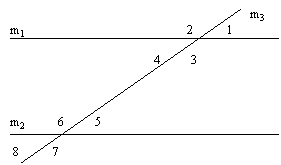
Supplementary Angles:
Two angles are supplementary is the sum of the
angles is 180o. Angles 1 and 2 as well as
angles 2 and 4 are supplementary angles.
Opposite (Vertical) Angles:
The intersection of two lines (m1 and m3) form 4
angles. Opposite angles are equal (congruent).
Angles 1 and 4 as well as angles 2 and 3 are
congruent.
Alternate Angles:
Lines m1 and m2 are parallel. Angles 4 and 5 are
alternate interior angles and are congruent. Angles
3 and 6 are also interior angles but are not
congruent. Angles 2 and 7 are alternate exterior
angles and are congruent. Angles 1 and 8 are also
alternate exterior angles but are not congruent.
Triangles:
The three angles of a triangle always total 180o.
An equilateral triangle is a triangle with 3 equal
sides and all 3 angles are 60o.
| An isosceles triangle is a triangle with
two equal angles. The two equal angles must
each be less than 60o. The image
on the left illustrates angles A and B are
equal. |
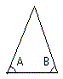 |
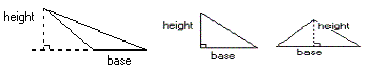
The height of a triangle is defined by the base.
Once any side of a triangle is chosen, the angle
between the base and height can change, but the but
measure of the height remains the same.
Back
to Top
Basic
Trigonometric Functions:
Trigonometry is a specialty of Geometry that
focuses mostly on angles. If we want the sum of all
internal angles or if we want a ratio of angles for
example, we will turn to Trigonometry.
Two recurrent terms to know are the Sine and
Cosine
- Sine = ratio of the height to the hypotenuse
(see image below)
- Cosine = ratio of the base of the hypotenuse
(see image below)
A simple example: A straight line has an angle -
its 0 degrees.
Sine = 00
Cosine = 10
To introduce the working formulas
for Sine and Cosine, we will use a right triangle.
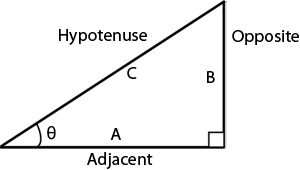
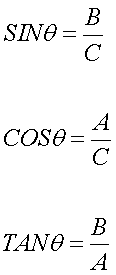
Pythagorean Theorem:
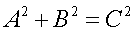
Sum of Interior Angles:
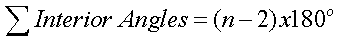
where n = the number of sides in the shape of the
object
Grade and Percent Grade:
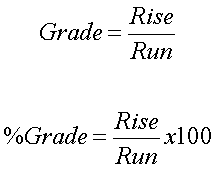
Back
to Top
|

