A logarithm is an exponent (power) to which a base
number must be raised to yield the same result. The
standard logarithm scale is called base 10.
The term "log" is used when specifying a log scale.
In base 10, the log of 100 = 2:
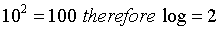
When basing your equation on base 10, indicating
the base is not required as base 10 is implied:
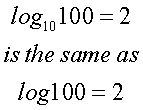
Other bases can be used, such as base 2, or base
3, or even base 25:
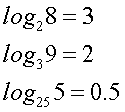
The reason for using a log scale is so we can
evaluate our data easier. For example, a chart of
data can either look like a boring straight line, or
with a log system applied, a more dynamic chart is
created:
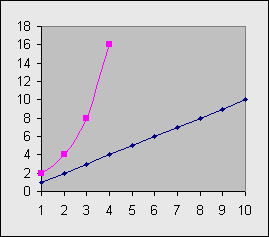
The graph above is nothing in particular, but the
blue line will be raw data, and the pink line will
be the same data using a base 10 log scale.
A perfect example of logarithm used
in Astronomy is the
Hertzsprung-Russell diagram, a
diagram of
stars.
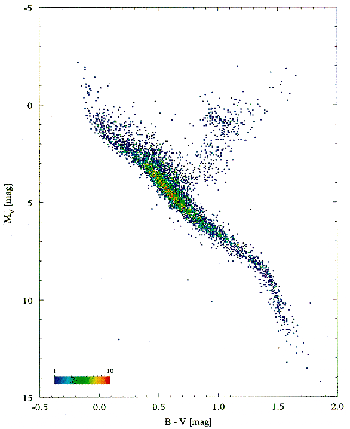
This diagram is an example of a
Hertzsprung-Russell
Diagram (H-R diagram). Astronomers already have the
data in log form, so an example of an
H-R diagram
with just raw data only is hard to find, but the
dots will reside in the lower half of the graph and
the curves will not be apparent. Back to Top |

