|
On the Stability of the Gliese 876 System of
Planets and the Importance of the Inner Planet - by Ricky Leon Murphy:
Back to Exoplanets
This is one of the major projects for the Swinburne
Astronomy Online Master's Degree Program. This is actually part two of my
two-part exoplanet subject. While both papers are not directly related to each
other, it does offer a look at both the amateur and professional involvement in
exoplanet research.
For part one,
Exoplanet Detection,
click the link.

Click for poster
Abstract
Introduction
Gliese876 and the System of Planets
Methods for Determining Mass Using High-Resolution
Spectroscopy
Orbital Dynamics
The N-Body Problem and the SWIFT Simulator
Solar System Simulations
Gliese 876 Simulations
Discussion
Summary
References
Abstract: A third planet with a mass of 0.023 MJ
was found orbiting the star Gliese 876. The initial two body system was found to
have a perfect orbital resonance of 2/1. This paper will demonstrate the orbital
stability to maintain this ratio is highly dependant on the presence of the
small, inner planet. In addition, any change in orbital eccentricity of the
inner planet as well as initial planetary set-up will also severely alter the
orbital dynamics of the remaining two bodies. In addition to this demonstration,
methods of detecting the planetary system will be covered as well as the
theories and techniques used to plot the orbits of these bodies.
Back to Top
1 - Introduction
A system of planets was found to orbit the star Gliese 876.
This is very unique as this is a class M star – the initial target of exoplanet
searches were G and K type stars. A class M star burns at a lower temperature
than our Sun, and is a third of the mass of our Sun. The
Astronomy Picture of the Day has a fairly un-impressive image of this star.
Equally unique is its distance, only 15 light-years away – Gliese 876 is one of
a handful of stars that is close to Earth.
This relatively un-impressive star is now host to three
planets, two of which orbit in a harmonious 2/1 resonance. The outer two planets
are what have been coined as “hot-Jupiters.” That is, giant Jupiter sized
planets that reside close to their host, and are therefore hotter in
temperature. The inner planet is one of the least massive planets ever detected
orbiting another star – at nearly 7.5 ME. This is an impressive feat
as the method used to detect these stars is high resolution spectroscopy from
telescopes here on Earth.
This paper will look at the stability of the current Gliese
867 system. The works of Innanen et al. [R9]
speculate as to the instability of our own Solar System minus the Earth-Moon
dynamic as well as without the inner Solar System. I will use this example to
determine the importance of the inner planet to the orbital stability of the
outer two planets of the Gliese 876 system.
Section 1.2 will cover the history of planetary detection of Gliese 876.
Section 2 will discuss the methods used to determine the masses of the
Gliese 876 members through high-resolution spectroscopy.
Section 3.1 will discuss the mathematics involved in determining orbital
dynamics and
Section 3.2 will cover the software used to implement these parameters and
discuss the method used to derive our results.
Section 4 will cover the actual simulation of our Solar System and the
effects of the inner planets while
Section 5 will cover the simulations of the Gliese 876 system. Following
these sections will be a
discussion as well as a
summary and opinion of results.
Back to Top
1.2 – Gliese 876 and the System of
Planets
The exoplanetary detection team led by Professor Geoffrey
Marcy is responsible for the majority of detected exoplanetary systems. This
team uses high-resolution spectroscopy from both the Lick and Keck
observatories. While the main focus of exoplanetary searches have been focused
on main-sequence G and K type stars, nearby M class stars have been included in
the search. Interestingly, the M class main-sequence stars make up almost 70% of
all stars in our galaxy [R16].
Gliese 876 is a class M4 star with a visual magnitude of
10.1. Its luminosity is 0.0124 LSun and mass of 0.32 MSun.
Using high-resolution Echelle type spectrometers – the Hamilton and HIRES – a
2.1 MJ mass planet was discovered orbiting Gliese 876 at a distance
of only 0.2 AU. Using Keplerian mechanics, the planet was found to orbit the
planet every 61 days [R16].
This data was reported to the Astronomical Journal on October 1, 1998.
Continual simulation by the Marcy team of Gliese 876
revealed certain issues with simulated data and observed results. After adding
Fourier components to the Keplerian mathematics, it was discovered that a second
body was responsible for explaining the simulated results. Since spectroscopic
data had continually been collected on this star since the 1998 report, the
Marcy team was able to compare the new simulation results with current observed
data. On July 20, 2001, a paper was published announcing Gliese 876 was host to
two bodies, the inner planet with a mass of 0.56 MJ and the outer
planet with a mass of 1.89 MJ. What’s more, these two planets are in
a 2/1 orbital resonance which is why the inner planet was undetected initially [R17].
Since the discovery, a host of papers have been written
about the simulation results of Gliese 876 in regards to its “perfect” 2/1
resonance [R2][R10][R11][R13][R14][R15][R20][R21].
In addition, simulations of this system are stable to a million years.
Instability in the system did occur with changes in eccentricity – which seems
to play a vital role in resonance – as well as changes in the initial position
of the planets prior to running the simulation [R20].
Ji et al. [R10]
states that orbital stability is very sensitive to the simulations initial setup
– that is the initial location of the two planets. In addition, the 2/1
resonance seems to occur and high inclinations and is vital to overall system
stability.
Laughlin et al. [R15]
and Zhou et al. [R24]
take the orbital simulations of Gliese 876 to a different level in that test
particles are inserted between Gliese 876 and the inner planet. The results seem
to support that a third body could exist in this region. A pre-print paper [R22]
was release just a few months ago the reveal a third body discovered between
Gliese 876 and the now middle planet. Labeled Gliese 876d, this planet is a
small ~7.5 ME body that orbits the host star at only 1.94 days. This
is the least massive extrasolar planet detected to date.
Table 1: Gliese876 System of Planets – 1998 [R16]:
|
Name: |
Gliese 876b (GJ876b) |
|
Mass: |
2.1 MJ |
|
Semi-Major Axis: |
0.21 AU |
|
Orbital Period: |
61 Days |
|
Eccentricity: |
0.27 |
Table 2: Gliese 876 System of Planets – 2001 [R17]:
|
Name: |
Gliese 876c (GJ876c) |
Gliese 876b (GJ876b) |
|
Mass: |
0.56 MJ |
1.89 MJ |
|
Semi-Major Axis: |
0.13 |
0.21 |
|
Orbital Period: |
30.1 Days |
61.0 Days |
|
Eccentricity: |
0.28 |
0.10 |
Table 3: Gliese 876 System of Planets – 2005 [R22]:
|
Name: |
Gliese 876d (GJ876d) |
Gliese 876c (GJ876c) |
Gliese 876b (GJ876b) |
|
Mass: |
0.023 MJ |
0.619 MJ |
1.935 MJ |
|
Semi-Major Axis: |
0.0208067 |
0.1303 |
0.20783 |
|
Orbital Period: |
1.94 Days |
30.34 Days |
60.94 Days |
|
Eccentricity: |
0 |
0.2243 |
0.0249 |
Back to Top
2 – Methods for Determining Mass
Using High-Resolution Spectroscopy
At this point of the paper, it is important to reveal the
techniques used to determine the mass of these (and other) extra-solar planets.
While mathematics and computer simulation are vital in this regard, there has to
be a starting point. Some of the introductory work in introducing the methods
used to detect extra-solar planets is found in a project paper I wrote for one
of my previous SAO classes, found here:
http://astronomyonline.org/Exoplanets/Exoplanets.asp.
To summarize, extra-solar planets are detected by one of
two main methods:
- Planetary transit
- Radial velocity
The radial velocity method – the method used to detect the
bodies orbiting Gliese 876 – makes use of a special type of spectrometer called
an Echelle. This spectrometer extends the focal length of the light while using
a very precise diffraction grating and high resolution CCD camera. This type of
spectrometer is capable of detecting radial velocity changes to 15 m/s. Further
improvements were possible with the introduction of an iodine gas over the
incoming spectra to serve as a composite spectrum. This technique improved
radial velocity changes to an astounding 3 m/s.
Detecting the mass of a planet orbiting a star using
spectroscopy is not a very accurate one, but does give Astronomers a starting
point to use in follow-up computer simulations to determine the orbital
parameters. Generally the only values that are given directly will be the mass
of the host star and an orbital velocity. Using a modified Doppler formula will
allow us to determine the mass:
 (1)[R19]
(1)[R19]
The mass of the planet is given in mpsin i
since we usually do not know the inclination. The value M is the mass of the
host star, P is the Doppler period and K is the semi-amplitude of the Doppler
shift. To solve for K:
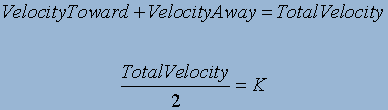 (2).
(2).
If we know the orbital period of the planet from radial
velocity measurements and we use equation 1 to determine the mass, we can
determine the semi-major axis by using Keplerian math:
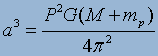 (3).
(3).
It should be noted that P should be converted to seconds
and mass should be converted to kilograms.
Using observational data, high-resolution spectroscopy and
Keplerian mathematics, it is possible to determine the mass of the star, mass of
the planet, the orbital period, and the semi-major axis. These values are enough
to insert into a simulation program to determine the other important orbital
characteristics – covered below.
Back to Top
3.1 – Orbital Dynamics
Orbital dynamics is a set of parameters that accurately
represent a system of planets. There are two variations of orbital dynamics:
Keplerian and Cartesian. Keplerian coordinates are a coordinate system based on
angles while the Cartesian coordinate system is based on points and vectors.
Both are a means to an end, their method of arrival is just a bit different. The
challenge of this paper is the literature used for reference uses Keplerian
coordinates while the simulation software used for this project (SWIFT) uses
Cartesian coordinates.
Keplerian Coordinates:
|
a |
semi-major axis of the ellipse – half of the major
axis of an elliptical orbit |
|
e |
eccentricity of the ellipse – where 1 is a straight
line and 0 is a perfect circle |
|
i |
inclination of the orbital plane – angle between
the orbital plane and a reference plane |
|
Ω |
longitude of the ascending node – angle between
line of nodes and the zero point of longitude in the reference plane |
|
ω |
argument of the pericenter – angle from ascending
node to the body in the orbital plane |
|
v (or f) |
true anomaly – location of planet from distance
closest to star |
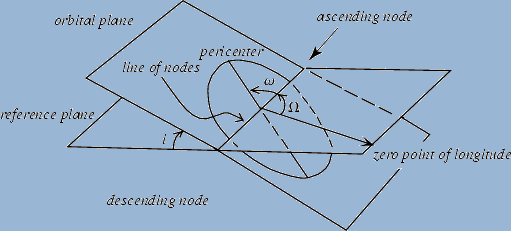
Figure 1
Figure 1 demonstrates the Keplerian coordinate system. One
of the issues with this project is the true anomaly. The orbital elements that
define the Gliese 876 system in the literature use a Mean Anomaly – which is the
average position of the planet over time. However, since the computer simulation
used for this project uses Cartesian coordinates, it is required to convert the
Mean Anomaly to the True Anomaly so a Keplerian to Cartesian conversion can take
place.
In order to make this happen, the eccentric anomaly must be
found. We are lucky in this regard as we have the value for the Mean Anomaly
given:
 (4)[R6].
(4)[R6].
Where M is the mean anomaly, E is the eccentric anomaly and
e is the eccentricity.
Once the eccentric anomaly (E) is found, we can use the
following equation to find the true anomaly:
 (5)[R6].
(5)[R6].
Where v is the true anomaly, e is the eccentricity and E is
the eccentric anomaly.
Now that we have all the values defined for the Keplerian
coordinate system, we can look at the Cartesian coordinate system – which is a
system of coordinates in a three-dimensional space.
Cartesian Coordinates:
|
X |
position of a point along the x axis – typically
horizontal |
|
Y |
position of a point along the y axis – typically
vertical |
|
Z |
position of a point along the z axis – or in and
out |
|
VX |
velocity of a point along the x axis |
|
VY |
velocity of a point along the y axis |
|
VZ |
velocity of a point along the z axis |
Both coordinate system offer both position and overall
orbital predictability – that is we can tell where an object will be as well –
or at least hope to be. These systems of coordinates do not take into account
the gravitational interactions between bodies.
There is a relation between both coordinate systems.
Relation between Keplerian and Cartesian Coordinates:
|
Keplerian: |
Cartesian: |
|
a |
X |
|
e |
Y |
|
i |
Z |
|
Ω |
VX |
|
ω |
VY |
|
v (or f) |
VZ |
Back to Top
3.2 – The N-Body Problem and the SWIFT
Simulator
In terms of the mathematics involved in solving for the
orbit of planets, a two-body system is the only system that can be solved
completely [R4].
The reason is that only two bodies are interacting with each other and the
forces are equal.
The following equations outline the 2-body problem:
 and and
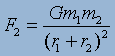 (6)[R1]. (6)[R1].
Since the only forces acting on each other are equal, the
2-body problem is completely solvable, without any need of mathematical
variations.
The 2-body problem above does not include other factors
required for simulating the two body system, but I will introduce them later.
An N-body system where N > 2 is not so easily solvable; in
fact there is no complete solution to the N > 2-body problem. The issue arises
with the mass interacting with each other – they are not equal:
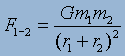 , ,
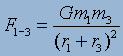 and and 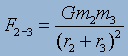 (7)[R4]; (7)[R4];
where F1-2 is the force between bodies 1 and 2,
F1-3 is the force between bodies 1 and 3, and so on. The above
example shows the forces of three bodies, but with additional bodies will add to
the complication of the system.
The forces of the N-body problem can be summed:
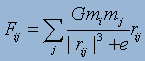 (8),
(8),
where n = i and j = n-1; n is the body. The value for e is
called the “softening” parameter and is programmed into the SWIFT code. This
allows a computer to compensate if the distance between two bodies gets too
close.
In addition to the forces exerted by each body, the tidal
forces must also be considered. A large central body – in our case, a star –
exerts a centrifugal force on the orbiting body. The orbit of this body while
feeling the force is called a Hill Radius:
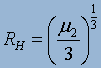 (9),
(9),
where μ is the reduced mass of the two bodies:
 (10).
(10).
In addition to calculating the forces, calculation of time
evolution and velocity is also required. For position:
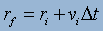 (11),
(11),
where rf is the final position, ri is
the initial position, vi is the initial velocity and Δt is the change
in time. For velocity:
 (12),
(12),
where vf is the final velocity, vi is
the initial velocity, F is the force exerted (equation 6) and Δt is the change
in time.
And finally, the system energy – that is both kinetic and
potential energy - must also be included in calculating the orbits:
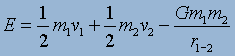 (13).
(13).
Notice the value for E is only for masses 1 and 2;
additional masses must have their own values, performed similar to equation 7.
This is a lot of calculation! For one body in a system in
one position, equations 8, 9, 10, 11, 12, and 13 must be performed. When the
planet moves into a new position, a new series must be solved. This is why
computer simulation is vital to simulating a system of planets.
Computer simulation software comes in a variety of styles.
Each code will utilize a specific style of mathematics to cope with the N-body
problem. While description of these styles is beyond the scope of this paper, I
will name a few as examples [R4]:
- The Lagrangian Solutions
- The Jacobi Coordinate System
- Sundman and Levi-Civita Regularization
- Tisserand’s Criterion
- Bulirsch-Stoer Method
- Fourth Order T-U Symplectic Method
- Regularized Mixed variable Symplectic Method
- Wisdom-Holman Mapping
In many cases, a particular software model will utilize two
or more of these methods as they can address specified portions of the N-body
problem.
Simulations for this project were performed using the SWIFT
package written by Hal Levison and Martin Duncan. This particular package
specializes in the use of massless test particles to study the effects by
massive objects while not interfering with the massive objects themselves. SWIFT
uses the following algorithms:
- Bulirsch-Stoer Method
- Fourth Order T-U Symplectic Method
- Regularized Mixed Variable Symplectic Method
- Wisdom-Holman Mapping
The Bulirsch-Stoer method attempts to extrapolate the next
step based on an initial step size[1].
The Fourth Order T-U Symplectic Method specializes in ecliptic orbits, but
cannot vary step sizes. The Regularized Mixed Variable Symplectic Method
specializes in close approaches to a massive body. And finally, the
Wisdom-Holman Mapping encompasses the standard N-body parameters with a feature
that corrects the orbit of Pluto.
SWIFT uses the Cartesian coordinate system for planetary
setup. It is also limited to initial runs of 1,000,000 years, but can continue
simulations beyond this point up to the limit.
The image below shows an example of the initial planetary
setup screen within SWIFT:
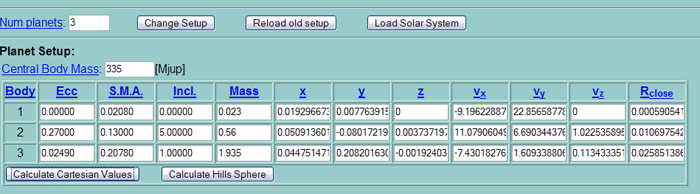
Figure 2
Test particles (figure 3) are required in the SWIFT
program, but the range is from 2 to 500 particles. The more particles, the
longer the simulation runtime:
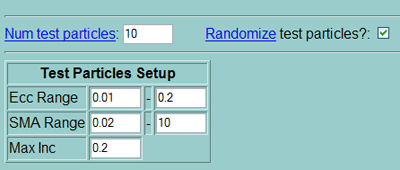
Figure 3
Finally, the parameters screen provides selection for the
runtime of the simulation:
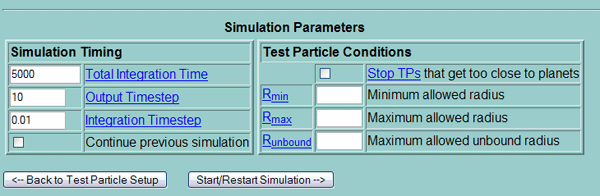
Figure 4
In the case of our simulations, test particles are not
required but a good sample (10) will allow for the simulation to continue
running in the event of planetary loss. In addition, the Integration Timestep is
also a very important parameter as most exoplanetary systems have their orbits
in days rather than years. A Timestep = 1 is an integration every year. In our
case, a Timestep = 0.01 gave more accurate results but this limits integration
time.
The Test Particle Conditions section is optional.
Back to Top
4 – Solar System Simulations
The works of Duncan & Quinn [R7]
and Innanen et al. [R9]
have demonstrated the long term stability of our Solar System out to a billion
years. As such, the simulations of the Solar System will not confirm the
obvious. Based on the works of Innanen et al. [R9],
I will demonstrate the necessity for long term stability of the orbital
eccentricities of the planets that include Earth and the inner Solar System.
While the eccentricities do vary, the results of such a change did not grossly
affect the overall stability of the Solar System as no bodies were ejected. It
is accepted that the gas Giant planets provide the gravity to keep the system
within the boundaries of the Solar System [R9].
The SWIFT simulator does contain the values for the 9
planets of the Solar System, but I found this lacking as the masses of the major
moons and of the asteroid Ceres are not included in the sample. I changed the
planetary setup to include 10 bodies, and moved the mass of the major moons to
their host planet:
|
Planet: |
Eccentricity: |
Semi-major Axis (AU): |
Inclination: |
Mass (in Jupiter-mass[2]): |
|
Mercury |
0.20563 |
0.9871 |
7.00487 |
0.000173919 |
|
Venus |
0.00677 |
0.72333 |
3.39471 |
0.002564386 |
|
Earth/Moon |
0.01671 |
1 |
0.00005 |
0.003185269 |
|
Mars |
0.09341 |
1.52366 |
1.85061 |
0.000338079 |
|
Ceres |
0.0789 |
2.767 |
10.58 |
0.000005026 |
|
Jupiter/ Ganymede/Io/Europa/Callisto |
0.04839 |
5.20336 |
1.3053 |
1.000208 |
|
Saturn/Titan |
0.05415 |
9.53707 |
2.48446 |
0.29949206 |
|
Uranus |
0.04717 |
19.19126 |
0.76986 |
0.048741297 |
|
Neptune/Triton |
0.00859 |
30.06896 |
1.76917 |
0.053964104 |
|
Pluto/Charon |
0.24881 |
39.48169 |
17.14175 |
0.00000768 |
While the simulations of the Gliese 876 system are
sensitive to the initial setup parameters of the Cartesian coordinates, this was
not the case in simulating the above Solar System. Once the masses were adjusted
to compensate for the large moons, and with the introduction of Ceres, a stable
simulation of the Solar System occurred 5 out of 5 times with random Cartesian
coordinates out to 107 years.
The first set of simulations includes all 10 bodies – the
color and number is to serve as a legend to the images:
- Mercury - Red
- Venus - Green
- Earth/Moon – Dark Blue (by serendipity)
- Mars – Aqua
- Ceres – Violet
- Jupiter and the four Galilean Moons – Yellow
- Saturn/Titan – Orange
- Uranus – Green
- Neptune/Triton – Blue-Green
- Pluto/Charon – Blue
The simulation parameters were out to 1,000,000 years but
the image below was constrained to a 100,000 year plot to allow the eccentric
variability to be visible:

Figure 5
The values of the eccentricities of each of the planets
above (figure 5) correspond well to the initial parameters. These results were
duplicated five times.
The second sets of simulations were run without the
Earth/Moon mass. This simulation included 9 bodies:
- Mercury – Red
- Venus – Green
- Mars – Dark Blue
- Ceres – Light Blue
- Jupiter and the four Galilean Moons – Violet
- Saturn/Titan – Yellow
- Uranus – Orange
- Neptune/Triton – Green
- Pluto/Charon – Blue-Green
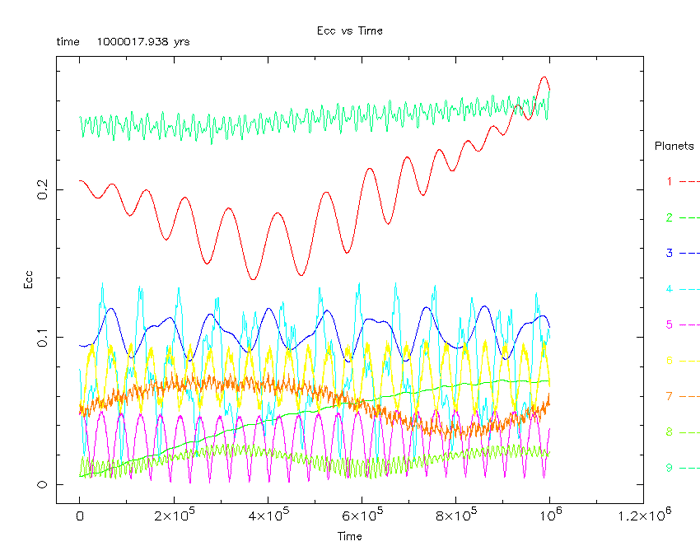
Figure 6
Again, this set of simulations (figure 6) was run five
times with equal results. There are noticeable differences already between Pluto
in the first simulation (Blue) and the second simulation (Blue-Green). Also,
the eccentricity of both Mercury (Red in both simulations) and Venus (Green in
both simulations) begins to get larger in this simulation. Pluto also begins to
migrate to a higher eccentricity.
The final series of Solar System simulations only included
Ceres and the outer planets:
- Ceres – Red
- Jupiter and the four Galilean Moons – Green
- Saturn/Titan – Blue
- Uranus – Aqua
- Neptune/Triton – Violet
- Pluto/Charon – Yellow
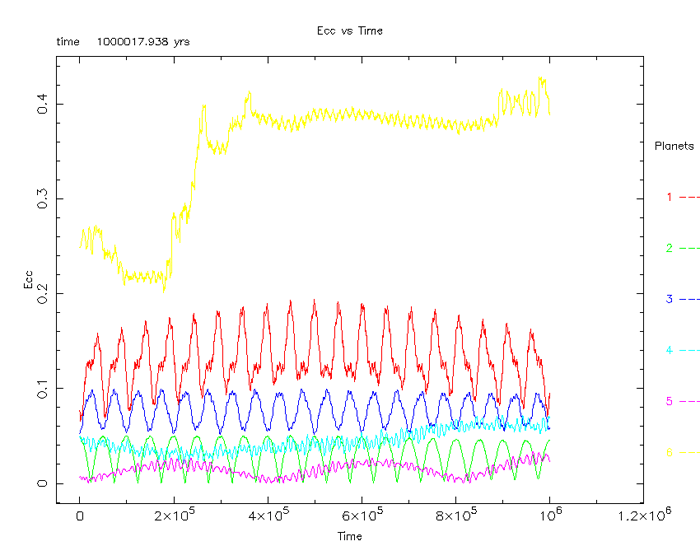
Figure 7
Immediately evident is the sharp increase in eccentricity
of the orbit of Pluto (figure 7). Additionally, Ceres begins to assume a larger
eccentricity as well.
The parameters for the Solar System series:
|
Total Integration Time: |
1,000,000 Years |
|
Output Timestep: |
5000 |
|
Integration Timestep: |
0.1 |
The test particles were random and set at 10. The test
particle output was not plotted for this result.
Back to Top
5 – Gliese 876 Simulations
The purpose of this paper is to determine the dynamical
stability of GJ876d – the newly discovered planet – has on the 2/1 resonant
stability of GJ876b and GJ876c. The gross computation of orbital resonance is
the ratio of the orbital period of two bodies, in this case, GJ876b and GJ876c.
With an orbital period of 61 days and 30.3 days respectively, both orbits can be
reduced to a ratio of 2/1 – or at least close to it. The laws of orbits are
applied here as the orbital duration is related to the distance the object is to
the host star. Having said that, determining to stability of the 2/1 resonance
of this system is the same as determining the overall orbital stability of the
system.
A painful lesson learned was that unlike our Solar System
simulations, the initial setup of the Gliese 876 system is vitally important.
Using Rivera et al. [R22]
as a starting point, I was able to determine the initial Cartesian coordinate
parameters. Given the time constraints of the project, I used an external source
[R26]
to convert the Keplerian coordinates – listed in the reference - to Cartesian.
Keplerian coordinates [R22]:
|
Coordinate: |
GJ876d |
GJ876c |
GJ876b |
|
a |
0.0208 AU |
0.13 AU |
0.2078 AU |
|
e |
0 |
0.2243 |
0.0249 |
|
i |
90 |
90 |
90 |
|
Ω |
not given (0) |
not given (0) |
not given (0) |
|
ω |
0 |
198.3 |
175.7 |
|
M – Mean Anomaly[3] |
309.5 |
308.5 |
175.5 |
Cartesian coordinates – converted [R26]:
|
Coordinate: |
GJ876d: |
GJ876c: |
GJ876b: |
|
X |
0.02079684 |
-0.0952695 |
-0.2022260 |
|
Y |
0 |
0 |
0 |
|
Z |
0.00032625 |
-0.0330609 |
0.01272650 |
|
VX |
-0.1208401 |
1.13349532 |
-0.1419209 |
|
VY |
0 |
0 |
0 |
|
VZ |
6.93269938 |
-3.2947981 |
-2.2445341 |
While the Keplerian coordinates provided by the literature
resulted in stable results by the authors, the converted results for use with
SWIFT was not successful. Two out of five runs failed to start while the other
three revealed the bodies settling in to highly eccentric orbits[4].
I am suspecting the conversion process is not entirely accurate. In order to be
epigrammatic, I have proceeded with my initial Monte Carlo simulations using
random parameters until a stable system presented itself.
The simulation parameters and test particle set-up remained
constant for the duration of the Gliese 876 simulations:
Test Particles:

Figure 8
Simulation Parameters:

Figure 9
The images below indicate a random selection of three
simulations I performed on the Gliese 876 system. Each of the simulations has a
different set of Cartesian coordinates, but the vital statistics are identical.
The planet setup – Random 1:

Figure 10
The result of a 1000 year plot:
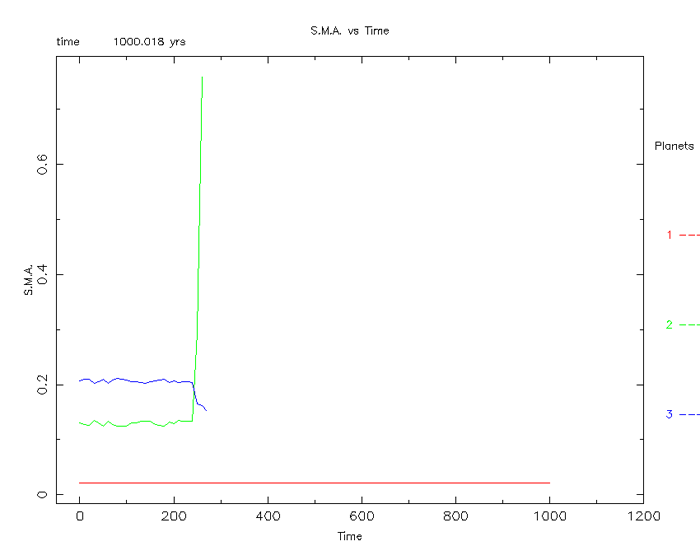
Figure 11
Almost immediately the two outer planets loose their
“resonance” and take on very different orbits (figure 11). The middle planet has
now become the systems outer planet as it quickly enters a large orbit. What is
interesting however is the SWIFT simulator does not indicate the planet as
“lost.”
The Planet Setup – Random 2:
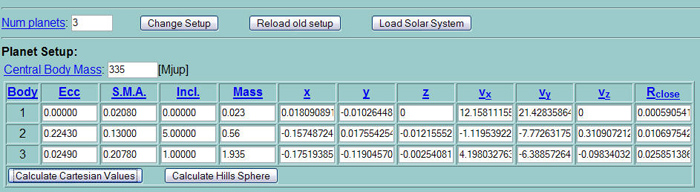
Figure 12
The result:
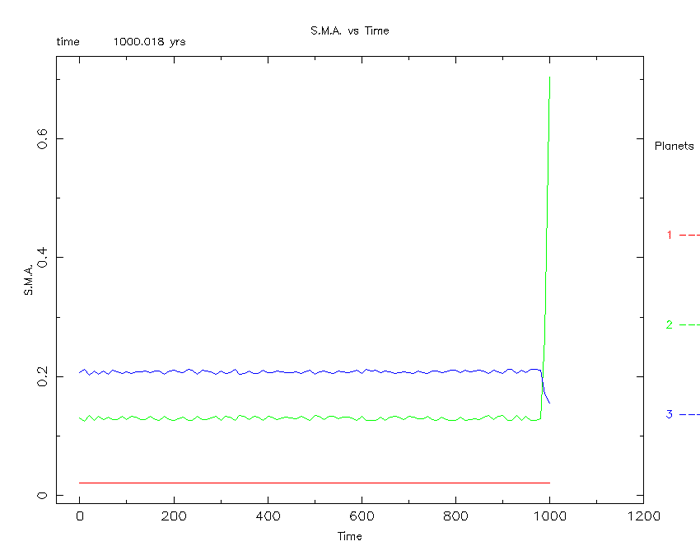
Figure 13
With only minor changes to the Cartesian coordinate set,
the two outer bodies do maintain a stable resonance up to 900 years (figure 13).
The end result is the same as the simulation above (figure 11).
The Planet Setup – Random 3:
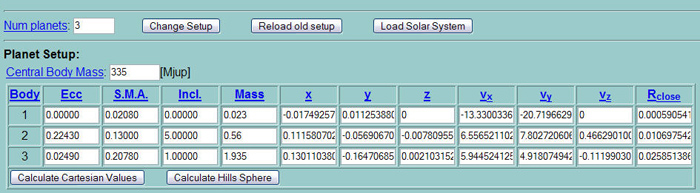
Figure 14
The result:

Figure 15
Our last random set and another change in Cartesian
coordinates indicate a very unusual and highly chaotic system (figure 15). This
type of orbit seems unlikely in reality.
It is clear the initial location of the planets prior to
running the simulation for this system is vital to overall stability. After
numerous Monte Carlo simulations of a variety of Cartesian sets, a stable
simulation was created:

Figure 16
The result:
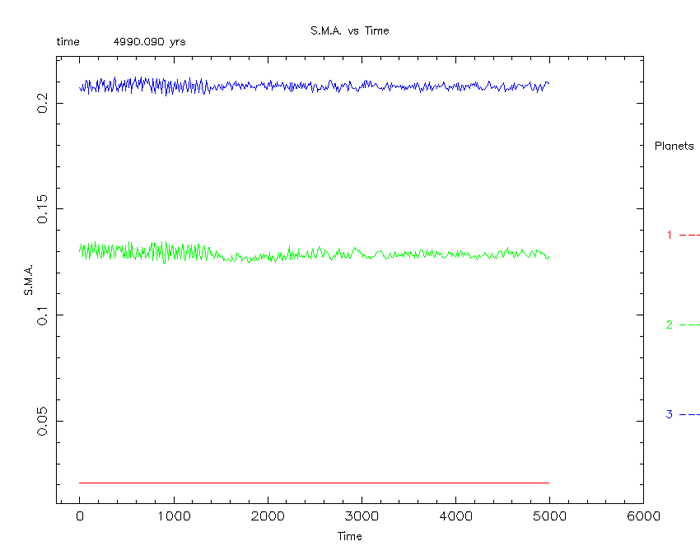
Figure 17
The image above (figure 17) demonstrates the stability of
the Gliese 876 system to the full 5000 year simulation. There are obvious
fluctuations indicated, but result from the natural resonant behavior of orbits
in close proximity.
Now that we have our parameters, the goal now is to
determine just how effective the inner planet is to the stability above. Keeping
the parameters equal to figure 16, only changes in planet 1 are made. The first
attempt is to reduce the mass of this planet. A simulation (figure 18) was run
with planet one at a mass of 0.0001 MJ.

Figure 18
The 5000 plot (figure 18) of this system reveals the inner
body’s incapacity to remain in its orbits. With the reduced mass of planet 1,
there is not enough counter-force keep the middle planet (planet 2) in
position.
Our second alteration of the mass or planet 1 is that of a
small asteroid. The following simulation (figure 19) was run with planet 1 with
a mass of only 0.000000001 MJ.

Figure 19
The 5000 year plot of this system with the further reduced
mass intensified the result of the inner planets incapacity to hold the middle
planet.
Various inclinations were explored in our Monte Carlo
Cartesian sets, but this does not cover eccentricity. The circular orbit of the
inner planet is also a stabilizing factor in this system. To demonstrate, the
following simulation (figure 20) is of the planet setup values in figure 16 with
only a change in eccentricity:
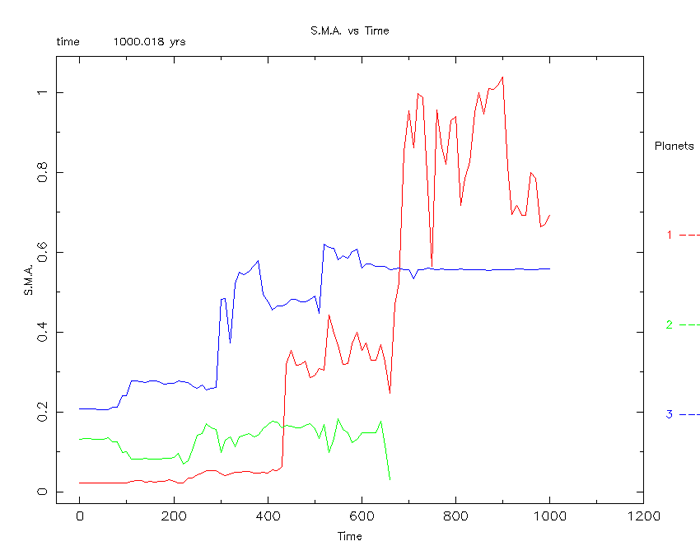
Figure 20
With an orbital eccentricity of planet 1 set to 0.1, it is
found that the Gliese 876 system is not stable at all.
Figures 16 and 17 indicate our stable system. The following
chart outlines the Cartesian coordinates and their counterpart Keplerian
coordinates through conversion [R26].
Cartesian coordinates:
|
Coordinate: |
GJ876d: |
GJ876c: |
GJ876b: |
|
X |
0.01929667 |
0.0509136 |
0.04475147 |
|
Y |
0.00776391 |
-0.08017219 |
0.20820163 |
|
Z |
0 |
0.003737197 |
-0.00192403 |
|
VX |
-9.19622887 |
11.0790604 |
-7.4301827 |
|
VY |
22.8565877 |
6.69034437 |
1.609338806 |
|
VZ |
0 |
1.02253589 |
0.11343335 |
Keplerian coordinates:
|
Coordinate: |
GJ876d |
GJ876c |
GJ876b |
|
a |
0.0208 AU |
0.13 AU |
0.2078 AU |
|
e |
0 |
0.2243 |
0.0249 |
|
i |
0 |
5 |
1 |
|
Ω |
0 |
275.688446 |
109.04065 |
|
ω |
-21.917107 |
25.256 |
31.0852 |
|
v |
359.999987 |
1.56104 |
0.09000802 |
Back to Top
Discussion
The presence of the inner bodies in both the Solar System
and the Gliese 876 system do affect the outcomes of the overall system dynamics.
In the case of our Solar System, there are enough bodies spaced apart – and with
significant mass – that our dynamic does remain in check but with changes to
orbital eccentricity. In the case of the Gliese 876 system, the “perfect” 2/1
orbital resonance of GJ876b and GJ876c is vitally dependant on the inner planet
– GJ876d.
Resonance is an important component of the Gravitational
Instability model [R24],
the model used to describe the evolution of the exoplanetary systems. Our Solar
System formed from the Solar Nebula Hypothesis. {During formation, these bodies
that would form planets are called planetesimals. They begin their life
as very small clumps of debris, but as the Solar Nebula contracts, a natural
disk shape forms (a result of the conservation of energy - a natural
phenomenon). These planetesimals assume their orbits and gather surrounding
debris in a process called sweeping. Because the terrestrial planets form close
to the proto-sun (the Sun at this point has not initiated fusion) the warmth
melts away any ices so rocky planets form. The Gas Giants are at a greater
distance and much of the ice and gas remains.}[5]
The problem with the Solar Nebula Hypothesis is that is
does not conform to any of the exoplanetary system that have been detected. The
Gravitational Instability model is designed to compensate for this. According to
this model, giant planet can form close to the host star but then settle into
greater orbits equal to that of our own gas giant planets. In some cases, the
movement of the giant planet can sweep up the necessary material to accumulate a
gaseous atmosphere – that is if the system is young enough. This model also
explains the resonant orbits of exoplanets as well: if two high mass planets are
formed close to each other, they can lock together in resonance and maintain the
same orbital dynamics for millions of years.
In the case of Gliese 876, the large bodies exhibit a 2/1
resonance – that is the middle planet – GJ876c - orbits at 30.3 days while the
outer planet - GJ876b - rotates at 61 days. It is believed the resonance of
orbits can save smaller bodies – for example Neptune and Pluto’s 3:2 that has
saved the smaller bodies such as TNO’s from ejection[6]
– but our simulations shows this is not the case for Gliese 876d. It is possible
that the 15/1 resonance of GJ876d and GJ876c provides the stability of GJ876c
and GJ876b, but this requires more simulation.
For the “perfect” 2/1 resonance to occur, the Gravitational
Instability model was probably working as the large bodies began their
migration. The inner planet could have provided the eccentricity required for
GJ876c to allow GJ876b and GJ876c to be captured in a co-rotational resonance [R3][
R24]. Once resonance occurred, it should be noted that there will be certain
libration to this resonance – in other words, each orbit may speed up or slow
down as each mass acts on each other [R3]
– similar to the action of a pendulum.
Back to Top
Summary
The lack of the Earth-Moon mass as well as the inner Solar
System greatly affects the orbit of Pluto in our simulations. With the benefit
of the gas giant planets of Jupiter, Saturn, Uranus and Neptune, the residual
bodies of the Solar System are still in check. The planetary system of Gliese
876 does not have the luxury of multiple large bodies to keep the system stable.
In fact, the orbital resonance of the two large bodies at such close proximity
relies heavily on the presence of the inner planet. There is enough mass within
the inner body to provide the counter-resonance required to keep this system in
check. It is difficult to say if the 15/1 ratio of the inner two bodies is
required for the 2/1 ratio of the outer two bodies - only with further computer
simulation can we determine this to be true – but the simulation results seems
to support this idea.
I would like to thank my supervisor, Professor James
Murray, for putting up with my endless simulation questions and for helping me
through the simulations of the Gliese system, and for help in understanding the
mechanics involved between the Keplerian and Cartesian system of coordinates. I
would also like to thank the Swinburne Astronomy Online group for providing the
material so this class could be taken and I would also like to thank the folks
over at the Swinburne Supercomputer section for allowing the students to run the
simulations required to complete this class.
Back to Top
References
[R1] Aarseth, Sverre. Gravitational
N-Body Simulations. Cambridge Monographs on Mathematical Physics, Cambridge
University Press. 2003.
[R2] Beauge, C.; Ferraz-Mello, S. and T.A.
Michtchenko. “Planetary Migration and Extrasolar Planets in the 2/1 Mean-Motion
Resonance.” ADS Pre-Print, April 2004.
[R3] Binney, James and Scott Tremaine.
Galactic Dynamics. Princeton University Press, New Jersey. 1987.
[R4] Boccaletti, D. and G. Pucacco.
Theory of Orbits. 1: Integrable Systems and Non-perturbative Methods.
Springer, Berlin. 2001.
[R5] Carpino, M.; Milani, A. and A.M.
Nobili. “Long-Term Numerical Integrations and Synthetic Theories for the Motion
of the Outer Planets.” Astronomy and Astrophysics, 181:182-194. 1987.
[R6] Carrol, Bradley and Dale Ostlie.
An Introduction to Modern Astrophysics. Addison-Wesley Publishing Company,
Massachusetts. 1996.
[R7] Duncan, Martin and Thomas Quinn. “The
Long-Term Dynamical Evolution of the Solar System.” Annual Review of Astronomy
and Astrophysics, 31:265-295. 1993
[R8] Hoi, Man and S.J. Peale. “Extrasolar
Planets and Mean-Motion Resonance.” Astronomical Society of the Pacific
Pre-Print, September 2002.
[R9] Innanen, Kimmo; Mikkola, Seppo and
Paul Wiegert. “The Earth-Moon System and the Dynamical Stability of the Inner
Solar System.” The Astrophysical Journal, 116:2055-2057. October 1998.
[R10] Ji, Jianghui; Li, Guangyu and Lin
Liu. “The Dynamical Simulations of the Planets Orbiting GJ 876.” The
Astrophysical Journal, 572:1041-1047. June 2002.
[R11] Ji, Jianghui et al. “The Liberating
Companions in HD 37124, HD 12661, HD 82943, 47 Ursa Majoris, and GJ 876:
Alignment or Antialignment?” The Astrophysical Journal, 591:L57-L60. July 2003.
[R12] Jones, Barrie W. and Nick Sleep.
“The Orbits of Terrestrial Planets in the Habitable Zones of Known Extrasolar
Planetary Systems.” Astronomical Society of the Pacific Pre-Print, November
2002.
[R13] Kinoshita, Hiroshi and Hiroshi
Nakai. “Stability of the GJ 876 Planetary System.” Astronomical Society of
Japan, 53:L25-L26. August 2001.
[R14] Kley, W. “Dynamical Evolution of
Planets in Disks.” Kluwer Academic Publishers. Netherlands, 2003.
[R15] Laughlin, Gregory et al. “The GJ
876 Planetary System: A Progress Report.” The Astrophysical Journal,
622:1182-1190. April 2005.
[R16] Marcy, Geoffrey et al. “A Planetary
Companion to a Nearby M4 Dwarf, Gliese 876.” The Astrophysical Journal,
505:L147-L149. October 1998.
[R17] Marcy, Geoffrey et al. “A Pair of
Resonant Planets Orbiting GJ 876.” The Astrophysical Journal, 556:296-301. July
2001.
[R18] Mayor, Michael and Pierre-Yves Frei.
New Worlds in the Cosmos. The Discovery of Exoplanets. Cambridge
University Press, 2003.
[R19] Pasachoff, Jay and Alex Filippenko.
The Cosmos: Astronomy in the New Millennium – Second Edition. Thompson
Brooks/Cole, Australia. 2004. (Note: material from this reference is from the
online bonus material, available to purchasers of the book only – and for a
limited time).
[R20] Psychoyos, Dionyssia and John D.
Hadjidemetriou. “Dynamics of 2/1 Resonant Extrasolar Systems Application to
HD82943 and Gliese876.” Kluwer Academic Publishers. Netherlands, 2004.
[R21] Rivera, Eugenio J. and Jack J.
Lissauer. “Dynamical Models of the Resonant Pair of Planets Orbiting the Star GJ
876.” The Astrophysical Journal, 558:392-402. September 2001.
[R22] Rivera, Eugenio J. et al. “A `7.5
Earth-Mass Planet Orbiting the Nearby Star, GJ 876.” ADS Pre-Print, 2005.
[R23] Snellgrove. M.D.; Papaloizou, J.C.B.
and R.P. Nelson. “On Disk Driven Inward Migration of Resonantly Coupled Planets
with Application to the System Around GJ876.” Astronomy and Astrophysics,
pre-print. April 2001.
[R24] Zhou, J.L.; Aarseth, S.J.; Lin,
D.N.C. and M. Nagasawa. “Origin and Ubiquity of Short-Period Earth-like Planets:
Evidence for the Sequential-Accretion Theory of Planet Formation.” The
Astrophysical Journal Letters, August 2005.
Back to Top
Image Credits
Figure 1:
http://scienceworld.wolfram.com/physics/OrbitalElements.html
Internet Resources
Astronomy Online:
http://astronomyonline.org/Exoplanets/Exoplanets.asp
[R25] SWIFT Website:
http://www.boulder.swri.edu/~hal/swift.html
[R26] Changing of the Elements:
http://janus.astro.umd.edu/orbits/elements/convertframe.html
[2]
The mass of Jupiter is 1.89 x 1027 Kg
[3]
See equations 4 and 5 for conversion from Mean Anomaly to True Anomaly
[4]
This failed simulations included both the given values for inclination
as well as the inclination values found in
figure 16.
[6]
This statement from my Astronomy 101 notes – Santa Barbara City College,
1995
Back to Top |

