Back to High Mass Stellar Evolution

Introduction
Overview of SNe Theoretical Models
One Dimensional Models
2-D Models
3-D Models
The Role of Stellar Rotation in Multidimensional Modelling & Observations
Nucleosynthetic Chemical Yields & Mass Ejection
Physics of Core Collapse Supernova
Nucleosynthesis of Type 1a SNe
Type Ib, c, II SNe Nucleosynthesis
Neutron Capture, Radioactive Decay and Observations
Particle & Neutrino Physics
Conclusion
References
Credits and Comments

Back to High Mass Stellar Evolution

Theoretical stellar models that attempt to reproduce supernovae (SNe¹) via core collapse processes are embodied in numerical simulations. Recent advances in our understanding of SNe processes as well as computer technologies both hardware and software, are producing increasingly sophisticated multi-dimensional SNe simulations attempting to reproduce observational results. Our discussion will contrast the different types of simulations used, associated input physics, reproduced chemical yields and ejected mass as well as key nucleosynthetic, particle physics and neutrino formation processes. In our discussion we’ll also attempt to correlate theoretical results with recent SNe observations and discuss the implications and futures of SNe theoretical models.

Back to Top | Back to High Mass Stellar Evolution

Modelling core collapse SNe is an active field of research that is rapidly maturing. It has been shown that Hydrodynamical bounce-shock energy transport following core collapse is on its own not sufficient to drive SNe explosions [7, 14]. Multidimensional simulations (2-d and 3-d simulations) representing theoretical SNe models have improved to the point where they are able to reproduce delayed explosions via neutrino driven energy transport and deposition effects. Multidimensional simulations still require approximations in input physics as technology and our understanding of the physical processes involved in SNe are evolving.

SNe stellar models attempt to simulate dynamic changes in stellar structure around core collapse time so that chemical yields, mass ejected and related explosive nucleosynthesis processes may be analysed. A simplified SNe structural model is shown in Figure 1:

Back to Top | Back to High Mass Stellar Evolution

One dimensional (1-d) models are spherically symmetrical, non-rotational representations of progenitor stars² which were originally pioneered in simulations by Colgate & White in 1966 [30] and Arnett in 1967 [31]. The basic foundations on which subsequent 1-d models evolved (as well as 2-d and 3-d models) were effectively provided by these authors. The Colgate, White & Arnett’s 1-d models used many approximations of neutrino-driven energy transport, neutrino physics as well as equations of state so as to demonstrate how SNe may be created.

Throughout the 1960’s and early 1970’s there were fundamental problems with 1-d models that precluded a physically complete description of core collapse SNe. There was a lack of realistic stellar progenitor models. There was also a neglect of weak neutral currents as well as uncertainties in the equation of state at super-nuclear densities [48]. Aside from input physics limitations from a technology perspective, there wasn’t any real ability to experiment beyond the spherically symmetrical, static (non-rotational) 1-d models.

Some of the characteristics of 1-d models include the emphasis on the neutrinodriven process as the means to drive the SNe explosion such that neutrinos emanating from the neutrinosphere deposit gravitational energy from the stellar core in the SNe mantle (see figure 1). Improvements in input physics relating to neutrino energy transport for instance using various Boltzmann solvers [7], has improved and provided a more accurate representation of the neutrino energy transport mechanism, however this hasn’t altered the overall imploding characteristics of 1-d models.

These characteristics are such that most 1-d models don’t demonstrate a net explosion and appear to fizzle into quasistatic accreting proto black holes [17] as shown in figure 2. Additionally, there doesn’t seem to be a widely accepted method that may contribute to the revival of the stalled shock observed after initial explosion. Even with up-to-date nuclear equations of state, neutrino physics such as accounting for the neutrino oscillation effect, improved stellar progenitor models, various implementation methods of 1-d simulations and up-to-date energy transport algorithms [23, 24, 25, 26] when using either a low or high entropy stellar core model, the energy coupling efficiency between the SNe core and mantle (core and mantle shown in figure 1) governed by neutrino-matter interactions is inadequate in 1-d models to prevent stalling of core-bounce shock explosion and its subsequent reignition. This leads to a recollapse even after a pause or ‘delayed’ re-ignition in 1-d models.

It’s evident also that this failure is consistent with various stellar progenitor models [17] such that varying the source model parameters doesn’t greatly affect the implosion outcome. The implications are clear. No explosions are generally observed in 1-d for Type I or Type II stellar progenitor models.

There has been evidence presented indicating that certain 1-d models do indeed show an overall net explosion after a delayed phase [32, 33, 34, 35]. These results are however controversial as neutron-finger convective instabilities and nuclear equations of state with high abundances of pions [7], used as methods to boost neutrino luminosities have been widely questioned by the astronomical [18] and nuclear physics [7] community, as they are seen to be unlikely contributors to the required energy deposition process required to drive and maintain SNe explosions.

Back to Top | Back to High Mass Stellar Evolution

Technological advances in the 1980’s coincided with pioneering SNe observations such as SN 1987A, which indicated anisotropies³ and large scale mixing of elements [14]. Armed with these constraining observations, 2-d models began to be used by some research groups aiming to overcome the stalled shock phenomenon observed in 1-d models [18]. One of the main differences of 2-d models when compared with 1-d models is that they take into account stellar rotation which brings on convection in the mantle region (figure 1). Figure 3 shows how rotational effects, more specifically the introduction of angular momentum, affects the entropy of theoretical SNe (shown in red).

Although 2-d models use similar input physics as 1-d models such as nuclear equations of state and neutrino nuclear cross-sections in calculations, compromises are generally made. For instance full neutrino transport is quite difficult to model in multi dimensional algorithms [7, 17], hence simple approximations in 2-d models are usually incorporated such as grey (spectrally averaged) energy transport and flux-limited, energy diffusion transport mechanisms [1, 3, 7].

Notwithstanding these approximations, initial results of 2-d models are promising, showing overall net explosions (as opposed to 1-d models) as indicated in figure 3. However 2-d (and 3-d models) are still not able to reproduce all the important observational signatures required to constrain and validate these models [17], which currently remains an outstanding problem in stellar astrophysics. We will explore some of these observational signatures later in our discussion.

A key difference brought about by rotationally induced convection of 2-d models is the efficiency of neutrino-matter coupling and the neutrino energy deposition rates observed in the results. Both of these are fundamentally related to stellar convection occurring in the ‘gain region’ (which is a thermal boundary in the mantle inside the shock front) [27, 41] where neutrino processes take place. Essentially in 2-d models, mantle convection makes the protoneutron star unstable. The resulting increase in entropy leads to a higher overall unstable core and mantle regions. All of this happens whilst processes outside the shockfront such as accretion and accretion induced luminosity continue to act against the shockfront. The net result after milliseconds from core bounce is a delayed SNe explosion [17]. Calculations performed in 2-d models point to a more unstable mantle due to convection; however this also appears to lead to weaker explosions when contrasted with observations [17, 28, 29]. It’s becoming clear however that the presence of convection, coupled with neutrino induced heating mechanisms ensures explosion of 2-d models [29].

Convection-induced perturbations in particle velocity and neutron excess (Y_e) can also alter the nature of 2-d core collapse models compared to the spherically symmetric 1-d models [3] favouring a SNe explosion. Explosive nucleosynthesis via neutrino induced heating in the oxygen layer at the bottom of the convection region where the forming proto-neutron star is located, also appears to be responsible for the success of 2-d explosion models [1]. Iron peak isotopes are created in this region such as Ni-56, responsible for powering SNe light curves. Explosive nucleosynthesis at the bottom of the oxygen convective shell is also responsible for the production of gamma ray emitting radionuclides such as Ti-44, Ni-57 and Co-56. Perturbations in neutron excess density and temperature that are left over from convective oxygen shell burning greatly affect the relative abundances of created isotopes. For example even the slightest change in neutron excess to the order of 10^(-4) can change the relative abundance of Fe-57 to Fe-56 by a factor of about 2 [3].

Recent advances in technology coupled with an improved understanding of the physics involved may allow neutrino transport to be handled in hardware and software using multi-group, multi-angle (Boltzmann solvers) techniques and also that hydrodynamical transport be handled in a similar way by means of solving general relativity equations [17]. Essentially this is about bringing more detailed microphysics into 2-d (and 3-d) models to avoid using approximations such as grey energy transport and flux-limited energy diffusion techniques. Preliminary results however don’t appear to significantly change from those of ‘conventional’ 2-d (and 3-d) models (those without the 1-d microphysics) which make use of energy transport approximations [2]. The implications of this may be that input microphysics may not add much more to the high level view of how SNe explosions take place and evolve, as opposed to rotation related effects.

Back to Top | Back to High Mass Stellar Evolution

3-d stellar models allow the representation of input physics and dynamic range required in a more comprehensive and holistic manner that may be performed in 2-d simulations. Based on 1-d and 2-d experiences, consensus in the astronomical community is that rotation and related effects induced, such as convection play a key role in SNe explosions [7]. It follows then that the need for 3-d simulations has been driven by the desire to more accurately model stellar objects in real life [6, 10], hence the requirement to use all dimensions available. This implies modelling a spherical body without boundary conditions [6] which is an inherent limitation of 2-d stellar models.

Besides the dynamic range and more accurate convection modelling available in 3-d, there are other relevant real-to-life processes that may be accounted for and more accurately modelled in 3-d, such as: explosion asymmetries which arise due to differences in convective regions [9]. Other SNe features that benefit from a 3-d treatment are convection asymmetries in the neutrinosphere [36], neutron star kicks [1, 21], magnetic fields, core fragmentation, convective instabilities, gamma-ray spectra produced and nucleosynthetic yields [10, 36]. In addition, angular momentum is also able to be more accurately modelled as it has been shown to pose constraints on convection efficiency, particularly in the equatorial region of progenitor models. It is important to note however that to achieve all this in 3-d within a reasonable timeframe requires hardware to be computationally expedient and software algorithms to achieve a balance between speed vs. additional sophistication required to consider these SNe effects.

Over the last 10 years 3-d simulation have provided results with interesting and at times controversial conclusions. For instance 3-d models of subsonic nuclear burning (deflagration models) in Type Ia SNe that have no adjustable parameters (such as initial flame geometry and multiple ignition spots outside the core as shown in figure 4) may produce weaker explosion energy models than 2-d Type Ia SNe counterparts. However nucleosynthetic predictions such as the produced masses of Nickel and ejecta velocities fall within acceptable observed ranges, unlike their corresponding 2-d models [5]. The implications of this for 3-d models and SNe Type Ia is that no fine tuning of the initial model is required in order to reproduce relevant observations as they relate to masses and ejecta.

When this is contrasted with Type Ib, c and Type II SNe a similar result is noticed in relation to explosion energy i.e. weaker explosions in 3-d models when compared to 2-d models [6] which is inconsistent with observations. Results also indicate that 3-d models may indeed produce higher explosion energies for Type Ia SNe [13] as opposed to Type Ib, c and Type II SNe. The dynamic nature of 3-d simulations introduce numerical uncertainties such as artificial density variations in the progenitor stellar model and numerical shear introduced by artificial viscosity typical in 3-d numerical algorithms [10]. Although further work is required in order to refine 2-d and 3-d models such as explaining the overall nature of delayed and weaker explosions, the outlook compared to 1-d models appears to be promising in relation to observations.

Back to Top | Back to High Mass Stellar Evolution

Aspects related to theoretical rotating stellar models are explosion asymmetries, increased and reduced convection in polar and equatorial regions respectively and assistance in providing and sustaining neutrino driven energy transport and energy deposition. These aspects are directly related to SNe observations.

Stellar rotation as a catalyst for convection and neutrino induced heating assists the expansion of SNe shock front in polar regions. Rotationally induced centrifugal forces resist gravitational collapse at the equator from mass accretion whilst increasing the efficiency of convection at the poles, hence easing the progression of the neutrino powered shock front in polar regions [7]. Although asymmetric SNe explosions may be of a delayed nature and lesser energy in rotating models (2-d and 3-d) the increased convection efficiency at the poles through rotation is able to greatly increase neutrino heating efficiency [1]. This results in explosion asymmetries.

Explosion asymmetry will cause deeper mixing in SNe ejecta and it has been shown also that polarization, as an observational signature [37] is consistent with asymmetric explosions [1, 37] in both Type I and Type II SNe. Hence asymmetric explosions of SNe may contribute to the extended mixing of elements and anisotropy observed. For instance observed extended mixing of iron peak elements may be explained by matter ejected along the poles with a much higher velocity as is the case in multidimensional rotational stellar models [37].

Rotational effects also appear to impact on overall neutrino luminosities. For instance non-rotating stellar models have larger neutrino luminosities as opposed to their rotating counter parts. This is due to non-rotating stellar core demonstrating an increase in gravitational compression as well as a large exponential neutrino energy effect due to temperature increase. For instance pair annihilation, which is a process that produces neutrinos begins at temperatures of 10^9 Kelvin [1]. The time of explosion is also earlier for a non-rotating stellar cores by a minimum factor of 2 [1].

Despite the differing results around explosion energies which require more experiments to fully resolve, it’s becoming clear that rotational models when compared to non-rotational models, induce asymmetries in SN explosions via convection, resulting in ejecta travelling faster at the poles than at the equator. This effect can be quite significant and is confirmed with given observations – the ratio of polar ejecta velocities to equatorial velocities may be in the order of 2 [1], consistent with theoretical results. Other aspects of neutrino processes consistent with convection resulting from rotation are an increase in luminosity from beneath the neutrinosphere, increased neutrino absorption close to the shockfront and energy transport and deposition occurring well away from the neutrinosphere [48]. These convection driven aspects assist in producing asymmetries and convection instabilities in theoretical multidimensional models.

Back to Top | Back to High Mass Stellar Evolution

Multidimensional simulations are able to assist in predicting chemical yields and mass ejected in the interstellar medium (ISM), however simulations need to consider two ways in which nucleosynthesis takes place in the context of stellar evolution and SNe. The first is conventional nucleosynthesis via fusion reactions occurring via the creation of heavier elements up to Iron resulting from increasing core temperatures during a SNe progenitor’s life. The second method is explosive nucleosynthesis which takes place when a hydrodynamical (Type Ib, c, and Type II SNe) or thermonuclear (Type Ia SNe) explosion occurs within the progenitor’s core. The most important one is explosive nucleosynthesis in the context of core collapse SNe.

Once a hydrodynamical or thermonuclear explosion takes place, a shock wave travels quickly from the core area outward into the adjacent inner stellar layers. Element creation via nucleosynthesis reactions takes place instantaneously as the travelling shock forces its way from the central core. Numerical simulations indicate that initially only elements residing in the core and adjacent inner layers are affected by explosive nucleosynthesis whilst leaving elements residing in the outer stellar layers relatively untouched by this process until the shock wave finally reaches the outer layers [38].

Theoretical stellar models that produce chemical yields and mass ejected as byproducts of SNe are dependent on contributing aspects such as input physics and explosive nucleosynthesis used. Each aspect has a range of parameters that astrophysicists need to carefully consider that will ultimately have a degree of impact on chemical yield produced and mass ejected. The following table shows an example of some of the parameters that require consideration for stellar models attempting to reproduce chemical yields and associated mass ejected:

As a result of the varying combinations that may be used in calculating chemical and mass ejection yields, it is common for results to vary, and in some cases even significantly [38]. As an example multidimensional simulations (2-d and 3-d) may provide yield differences compared with 1-d simulations which although negligible for light elements, are somewhat noticeably different for heavier elements [11, 12]. This is generally attributed to the consistently higher temperatures produced by multidimensional simulations in the inner core induced by stellar rotation (hence convection related effects), which leads to higher core neutronization (neutron and neutrino production). Core neutronization assists in the production of isotopes that are very sensitive to neutron capture such as those of Calcium, Titanium, Vanadium, Chromium and Zinc [11].

It is important to note however that amongst the differences in chemical yields and hence mass ejected between models and various approaches to input physics, there are commonalities. For instance in hydrodynamic explosions characterised by Type Ib, c & Type II SNe one group of elements, which include Oxygen, Neon and Magnesium are not generally affected by explosive nucleosynthesis. These elements are created in the outer layers well away from the ignition point during conventional nucleosynthetic processes. This group of elements have yields proportional to the mass of the progenitor star and not dependant on explosive nucleosynthesis. It follows then that massive hydrodynamically ignited SNe eject more elements from the outer layers than less massive SNe of the same type. Conversely another group of elements that include Iron, Calcium, Sulphur and Argon are produced as a direct consequence of explosive nucleosynthesis and to a degree are less dependent on progenitor mass [38, 11].

Figure 5 summarises work performed by various research groups in providing Oxygen and Iron estimates for theoretical Type II SNe, which we’ll use as indicative examples of elements in the two groups described earlier. One can clearly see that for Oxygen the mass ejected on the y-axis in solar masses, as a function of progenitor mass (x-axis) clearly increases across all models used. This is in contrast to Iron mass ejected for each computed model, indicating that for Type II SNe, Iron doesn’t readily pollute the ISM and is retained as part of the post-explosion stellar corpse.

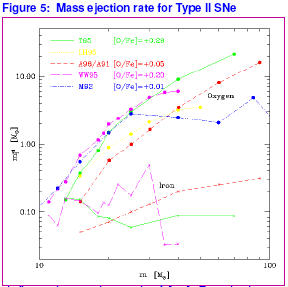
These theoretical results from modelling can be contrasted with observations such that they may be validated in order to constrain or otherwise the contributing aspects of multidimensional input physics and explosive nucleosynthesis.

Recent multidimensional modelling of Type Ia SNe such as those shown in figure 4, have made use of nonadjustable inputs for simulated thermonuclear explosion processes(as opposed to 1-d models) in order to examine chemical yields and mass ejection quantities as a function of explosion type such as deflagration or detonation⁴ [12]. Results have shown that large amounts of Iron are produced and that the core Carbon-to-Oxygen (C/O) ratio in Type Ia SNe progenitors affects the amount of Ni-56 produced (the more unburnt Oxygen remains, the less Ni-56 created) which has implications not only for chemical yields and related mass ejected, but also for Type Ia SNe energy generated and detected via light curve analysis [39].  Consequently it’s reasonable to assume that chemical yields produced, energy generated and mass ejected are a function of progenitor composition, temperature and nucleosynthesis for Type Ia SNe [12].

Theoretical multidimensional models and observations for ionised Iron in Type Ia SNe are generally consistent [4]. Multidimensional models of Type Ia SNe have shown also that much larger fractions of unburnt Carbon and Oxygen are retained after a thermonuclear explosion by the ISM (up to as high as 50%) which is 2.5 times more than 1-d simulations [12]. Light curve observations provide the ability to constrain or otherwise these results produced [22, 39] which appear to be high in multidimensional models compared to observations [4, 20].

Advances in multidimensional models are able to provide an insight into certain elements that are very sensitive to explosive nucleosynthesis such as Ni-56 and Ti-44. Both these elements are extremely important for the evolution of SNe remnants and for the subsequent chemical evolution of galaxies [11]. Elements such as Ni-56 and Ti-44 are also useful as ‘simulation probes’ as their yields and mass ejection rates can assist in constraining numerical models, more specifically hydrodynamical effects and neutrino-matter interactions, which ultimately assist in better understanding thermonuclear (Type Ia SNe) and hydrodynamical (Type II SNe) explosions.

Although substantial work has been done with 1-d and multidimensional simulations in an attempt to reproduce observations, more work is required to further refine these models. An example of this is the neutron excess (Y_e) problem. Y_e is constrained by nucleosynthesis and is generally higher than allowed for 1-d models and higher again for multidimensional models infact, Type Ib, c and Type II SNe 2-d and 3-d models leave behind neutron stars which are lower in mass than observations put forward [48]. This suggests that other input physics and/or explosive nucleosynthesis considerations need to be accounted for to take this observational aspect into account [1].

Although there are discrepancies in 1-d and multidimensional results and observations as they relate to yields and mass ejected, improved 3-d modelling techniques are thought to be able to reduce the discrepancy between theory and observations such that more efficient burning of the theoretical C/O core may take place [19] as an example. Notwithstanding discrepancies, the general consensus in the astronomical community appears that 3-d simulations (given their ability to better represent dynamic range and “real life” effects) are able to more faithfully reproduce chemical yields, mass yields and observed light curve spectral features than 1-d or 2-d models [4, 19], hence this sets the scene for the future of 3-d simulations as the bridge between theory and observations.

Back to Top | Back to High Mass Stellar Evolution

It is appropriate at this point to discuss relevant nucleosynthesis, particle physics and neutrino ⁵ processes with particular focus around core collapse events. Type Ia and Type II (including Type Ib, c) SNe explode via thermonuclear and gravitationally induced core collapse respectively, and each also undergo conventional and explosive nucleosynthesis⁶ before and after core collapse. These will be covered for each SNe type in conjunction with relevant particle physics and neutrino processes. Differences will be highlighted where appropriate in the following discussion.

Element nucleosynthesis via fusion processes in Type Ia SNe (progenitor solar mass < 8 solar masses [38]) is able to produce elements up to Carbon as shown in figure 6. Key fusion reactions responsible for the stellar structure in figure 6 are the Proton-Proton chain and the Carbon-Nitrogen-Oxygen chain, simply described in table 2 as follows:

Both the PP and CNO reactions occur at increasingly higher core and inner layer temperatures. These reactions are able to produce heavier elements in respective layers closer and closer to the core as shown in figure 6. At a point at which electron degeneracy doesn’t allow pressure to increase further, the C/O core temperature continues to increase until it explosively ignites via detonation and/or deflagration [12]. At this point explosive nucleosynthesis along with neutron capture [42] is responsible for the production of radioactive isotopes of elements such as Silicon, Nickel, Titanium and Iron, which are subsequently ejected in the ISM [12].

Although neutrino processes occur during conventional and explosive nucleosynthesis, neutrino energy deposition plays a small part in powering the explosion of Type Ia SNe, given that neutrinos easily disperse away from the stellar core [49]. Radioactive decay of elements via gamma ray and beta decay occur [44] which contribute to the observed energy deposition rates, chemical and mass yields and element abundances detected in Type Ia SNe light curves.

Back to Top | Back to High Mass Stellar Evolution

When the Type Ia SNe scenario is contrasted with more massive progenitor stars (Type Ib, c & Type II SNe) we find a different structure and more evolved conventional nucleosynthesis before core collapse. Element nucleosynthesis via fusion in progenitor stars with solar mass > 10 solar masses [38] are able to produce elements up to Iron as shown in figure 7 below. The key fusion reactions (in their simplified form) which occur with increasing core and inner layer temperatures are shown in table 3 as follows:

Once the Iron core is formed, neutrino processes in Type Ib, c & Type II SNe (unlike Type Ia SNe) become very important. As neutrinos are transparent to the stellar core they radiate away, leading to photodisintegration of the core which results in further gravitational core collapse. Ultimately this leads to core rebound at nuclear density generating a shock wave powered by a second wave of neutrinos which meets gravitationally infalling matter. At this point explosive nucleosynthesis takes place, freezing out the newly created elements via numerous nuclear reactions. Elements are created such as Nickel, Titanium, Cobalt and Sodium. These and other radioactive isotopes created via neutron capture processes, decay with varying ½ lives. Subsequently energy released in element decay, powers observed SNe light curves which are used to spectroscopically determine element abundances, energy deposition rates in circumstellar material, chemical yields and mass ejection rates.

Back to Top | Back to High Mass Stellar Evolution

During a SNe explosion neutron capture takes place which can occur via the slow process (s-process) or via the rapid process (r-process) [40]. The neutron capture rate (slow or rapid) is determined relative to competing beta decay rates. Hence in the s-process neutrons are captured slowly by elements relative to the beta decay rates and in the r-process neutrons are captured faster by elements relative to beta decay rates. Although both these processes occur in SNe, the r-process dominates over the s-process meaning that neutron capture is extremely efficient. This is demonstrated in both 1-d simulations [42] and multidimensional simulations [6,16], and is also thought to be responsible for the majority of existing elements beyond Iron as shown in the periodic table [43]. The r-process is also responsible for producing some of the heaviest elements such as the transuranic elements beyond Bi-209 [40], which is not possible by the s-process. The following table shows the generalised nuclear reactions for each competing processes namely neutron capture and beta decay.

A key radioactive decay process which follows explosive nucleosynthesis in both Type I and II SNe is Ni-56 -> Co-56 -> Fe-56, which is responsible for gamma ray and beta decay energy deposition in SNe light curves. This reaction is directly responsible for sustaining the energy observed in SNe light curves.

It’s important that if theory is to be validated by observations, that simulations (particularly multidimensional simulations as these have so far demonstrated to be able to better predict observations [15]) improve to the point of homologous expansion [8] so that synthetic spectra produced via initial conditions can be reasonably verified with observational SNe light curves.

To this end various research groups [5, 12, 13, 15] are undertaking this task. Figure 8 shows synthetic light curves (solid black) vs. observed light curves (dotted green) for Type Ia SNe. In general the synthetic approach is on the right track, however more work is still needed to explain discrepancies and required to fine tune synthetic spectra.

Back to Top | Back to High Mass Stellar Evolution

Several particle⁷ and nucleon⁸ processes in SNe physics contribute to neutrino production, absorption and neutrino scattering. These processes are particularly important for heavier stellar progenitors of Type Ib, c, and Type II SNe around core collapse time as neutrino interactions are essential in producing and powering SNe explosions.

An important producer of neutrinos is neutronization⁹ which is a nucleon process based on electron capture. At the point of nuclear degeneracy and core bounce in SNe, neutronization recombines protons and electrons to create neutrons and electron-neutrinos (free protons and electrons in the core exist as a result of photodisintegration). Neutronization occurs alongside electron-antineutrino production which is another electron capture process, whereby electrons combine with neutrons to create electron-antineutrinos and protons inside the gain radius. These two processes cool the outside of the forming proto-neutron star as neutrinos diffuse away from the core. This is shown in table 5 and figure 9 where it’s described as the ‘cooling’ region.

Outside the gain radius neutrinos encounter high opacity at the shockfront due to expanding and infalling matter meeting at this point¹⁰. This zone, called the heating region (see figure 9) is where neutrino absorption takes place (as shown also in table 5).

SNe energy gained by neutrino absorption in the heating region is greater than energy lost by electron capture in the cooling region [41]. Hence energy deposition via neutrino absorption in the heating region is a key factor in driving and reviving stalled SNe shocks that attempt to propagate in adjacent stellar layers. It follows that electron capture (which includes neutronization) inside the gain radius (figure 9) in the cooling region and neutrino absorption in the heating region, play a key role in SNe.

Nucleon based interactions such as the modified URCA processes [46] also contribute to the production, scattering and absorption of neutrinos in the cooling and heating regions. Other particle processes which play a role in these regions are pair annihilation, plasmon decay, the Photoneutrino process and Bremsstrahlung. These processes are shown in tables 6 and 7 respectively:

The processes listed in tables 5, 6 and 7 hide the importance of each reaction type and types of neutrinos produced. For instance there are electron, muon and tau neutrinos created, however the electron-neutrino flavour dominates in these nuclear reactions as more of them are created. Additionally the most prevalent neutrino production processes in SNe are Bremsstrahlung, the Photoneutrino process and those related to electron capture (including neutronization) and absorption [45], as these are dependent on the high temperatures and densities found around SNe core and shock fronts. There are also neutrino interactions which involve neutrino scattering in the heating and cooling regions of SNe as shown in table 8:

A summary of these processes is provided in table 9. It is estimated that 10^53 ergs of energy [47] are released in a SNe explosions hence important neutrino production and absorption processes (highlighted below) play a key role in this vast amount of energy produced:

Our understanding of SNe physics such as explosive nucleosynthesis and neutrino processes and our ability to exploit single and multidimensional modelling techniques to reproduce these effects is maturing rapidly. It is clear now that neutrino physics plays a key role in producing and sustaining SNe explosions and that explosive nucleosynthesis is responsible for the production of various elements found in the interstellar medium. It is also becoming clear that processes such as neutron capture as part of explosive nucleosynthesis, beta decay and neutrino physics are bridging the gap between theory and observations.

Although multidimensional chemical yields, energetics and delayed explosions are only partially solved, 3-d SNe models hold the key to required improvements in results relating to rotation, convection and ejecta asymmetries which correlate with results of observed light curves and derived chemical and mass yields. Further improvements in microphysics being groomed in 1-d models is expected to be used to complement multidimensional models so to provide a holistic view of the SNe core collapse processes. In addition further observations, analysis and results will continue to provide constraints for theoretical models and this will assist in further bridging the gap between theory and observations.

Back to Top | Back to High Mass Stellar Evolution

References:

[1] Fryer C. L., Heger A., 1999, Core-Collapse Simulations of Rotating stars, http://arxiv.org/abs/astro-ph/9907433

[2] Livne E., Burrows A., Walder R., Lichtenstadt I., Thompson T. A., 2003, Two-Dimensional, Time-Dependent, Multi-Group, Multi-Angle Radiation Hydrodynamics Test Simulation in the Core-Collapse Supernova Context, http://arxiv.org/abs/astro-ph/0312633