|
Gravitational Lensing - by Ricky Leon Murphy:
Introduction
A Gravitational Lens
The Gravity Lens in Use
Gravity Lens and Dark Matter - Microlensing
Gravity Lens and Dark Matter - Weak Lensing
Gravity Lens and Dark Matter - Strong Lensing
Summary
References
Web Sites
Image Credits
Back
to Cosmology
Introduction:
The breakthrough of
Einstein’s General and Special Theories of Relativity give us a much
clearer picture of some of the observed and theoretical processes within
the Universe. Much of his theories have already been confirmed by
observation including the bending of light waves by a massive object.
Such proof was witnesses as stars near the Sun were shown to shift
positions – observed during a solar eclipse. On a much larger scale,
massive objects like black holes and brown dwarfs also bend distant
light rays as do galaxies and galaxy clusters. When using massive
objects like galaxies and galaxy clusters to examine the bending of
these light rays, the gravity of these objects acts like a lens. This
effect is called gravitational lensing and has proven very effective in
observing some of the most exotic phenomenon such as exoplanets and
quasars. Even more remarkable is the use of gravitational lensing to
detect and map dark matter regions surrounding galaxies and galaxy
clusters. By using a gravity lens, the detection of dark matter has been
confirmed and is providing valuable data for cosmologists to help mold
the theories involving the constituents and origins of dark matter.
Back to Top
| Back to
Cosmology
A Gravitational Lens:
The presence of mass
within space-time creates a curve (or depression) in the fabric of
space-time. The common analogy of this is the rubber sheet.
|
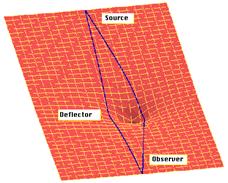
Figure 1. |
Figure 1 shows an
example of the rubber sheet, with a mass – that is invisible in
this example – that has created a depression within space-time.
As light waves (indicated in blue) pass close to the curved
space, its path is altered resulting is a bending of light. For
the lens to work properly, the source of the light must be in |
the line of sight to the
observer with the massive object in between. This basic two dimensional
lens demonstrates a correlation between length and angles based on the
radius of influence by the massive object.
|
Figure 2.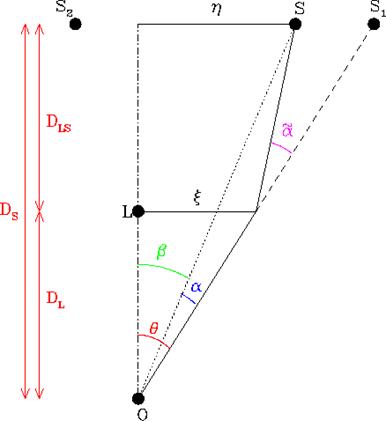 |
|
Figure 2 is a
graphical example of this two dimensional lens. The point L is
the massive object while point S1 is the distant object. S is
the apparent position of the object to the observer; O. S2 is
ignored in this example. This equation (right) demonstrates the
basic properties of the lens effect in figure 2 (the following
examples: Wambsgauss, 2001). |
 |
It is important to state
that several correlations exist with the basic lens equation that
carries over to real world examples. The length to the lenses object is
correlated to the distance to the lensing object (L) by the following
equation:
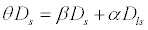
This directly translates
to a correlation to the angles involved:
.
This is an important
realization as this gives astronomers a tool for measuring the strength
of a gravity lens with the benefit of helping to determine the distance
as well.
As a summary, the above
example can be put together to form the Einstein Radius, the radius of
influence by the lensing object:
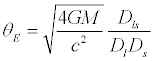 . .
So what would a gravity
lens look like for a familiar object?

Figure 3.
The above image
demonstrates what an invisible mass would do if placed between us and
the Mona Lisa. The point source is tiny with a mass of the planet
Saturn. Notice the obvious circular effect of the lens – the radius.
Also notice the tiny nose and the small arc of the mouth within the
radius. The overall image is also bloated – spread out as a result of
the lensing. This is a typical effect of the gravity lens.
Back to Top
| Back to
Cosmology
The Gravity Lens in
use:
On September 13, 1990,
the Hubble Space Telescope issued a press release of what is probably
the most famous of all images of a gravity lens:

Figure
4.
This particular
arrangement is called the Einstein Cross. The four points of the cross
are a lenses distant quasar, 8 billion light years away. The center if
the cross is the lensing body, a galaxy “only” 400 million light years
away (http://hubblesite.org/newscenter/newsdesk/archive/releases/1990/20/image/a).
The gravity lens is used
to study a variety of phenomenon, and is separated into three groups (http://astron.berkeley.edu/~jcohn/lens.html
):
- Strong Lensing
- Weak Lensing
- Microlensing
Strong lensing is the
result of a lensing object splitting the lensed object into separate
distinct images – like our Einstein Cross example above. Strong lensing
can also produced a large number of arcs as well. The usual targets for
strong lensing are clusters of galaxies. By studying the strength of the
lens, the astronomers learn about the mass distribution throughout the
cluster.
Weak lensing is defined
by arcs of the lensed object by a lensing object.

Figure
5.
This Hubble Space
Telescope image of galaxy cluster Abell 2218 shows an example of weak
lensing, the arcs of distant galaxies lensed by the cluster. Studying
weak gravitational lensing is very useful in the study and detection of
dark matter.
Microlensing is also a
gravity effect, but not as pronounced as strong or weak lensing. In this
case, the lensing mass is a MACHO (Massive Compact Halo Object) – black
holes, white dwarfs, brown dwarfs. The result of a microlens is a
momentary increase in brightness of a distant object. A type of baryonic
dark matter (although only a small percentage of dark matter) are
MACHO’s, so mapping the distribution of these objects is useful in the
study of dark matter (Silk, 1999). Microlensing has also been effective
in the detection of exoplanets as well, but that is another story.
Back to Top |
Back to Cosmology
The Gravity Lens and
Dark Matter - Microlensing:
For the duration of this
paper, we will focus on microlensing and weak lensing and its
effectiveness in the detection and study of dark matter (although a
brief entry of strong lensing will occur later on). The nature of dark
matter is such that direct observation is not possible but direct
detection is possible. We know of its existence by the nature of the
gravity lens as well as rotation curves of spiral galaxies. Careful
study of gravitational lensing helps astronomers determine the type of
dark matter in existence as well as mapping its distribution – the
gravitational lens is the fundamental test in the nature of dark matter
(Metcalf and Silk, 1999). While the scope of this paper is not to
determine what dark matter is – MACHO’s, Cold Dark Matter, Warm Dark
Matter or other form of non-baryonic dark matter – but to determine its
ability to affect a gravitational lens. The fundamental test for dark
matter is using the gravity lens to map the distribution of this
material through a modified form of the Einstein Radius equation:
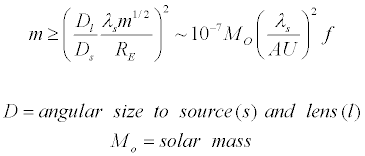 . .
This equation may seem
rather complicated, but according to Metcalf and Silk, 1999 this
equation is used for a point source such as a supernova. The implication
is that a mass of an exploding star is known so with the strength of the
lensed supernova (granted one is in the right spot), the mass and radius
of the lens determines the nature of the lensing material – in the case
of Metcalf and Silk, 1999, either MACHO’s and/or interacting elementary
particles (possibly neutrinos).
What is unique about
microlensing is its ability to pinpoint sources for direct detection.
For example, very bright stars in distant galaxies can be lensed by
local massive objects in order to determine the mass of the lens source.
A relic massive black hole is presumed to be an example of a MACHO (MAssive
Compact Halo Object), and very strong lensing of an individual star was
detected to show single objects that collectively give a total universal
mass density of 0.4 – which is determined by the probability of
microlensing events (Turner and Umemura, 1997). Two gravitational
microlensing surveys were performed to map out the distribution of
MACHO’s near the galactic bulge and the Large Magellanic Cloud (LMC). By
continuous telescope searches from two locations, it was possible to
perform real-time spectroscopic data on these microlensing events (Alcock
et al., 1996). The spectroscopic data would determine the nature of the
lensing object. Because the galactic bulge and LMC were chosen, the
likelihood of MACHO detection was more likely (Alcock et al., 1996). The
equation for determining the Einstein Radius for the MACHO survey is a
bit different:
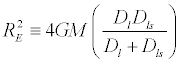 . .
This variation of the
equation is almost elegantly simple and has some added benefits:
- If we know the
distance (D) to the lensed object (ls) and the lens (l),
we can determine mass
- If we know the mass
of the lens as well as distance, we can determine distance to the
lensed object
all of which to a good
approximation.

In
the case of this specific MACHO survey, the lens is predominantly brown
dwarf stars. While technically a MACHO (brown dwarfs reside in the halo
and it is a compact object), it is unlikely that brown dwarfs contribute
any significant mass to dark matter. The figure above (http://www.llnl.gov/str/June03/Cook.html)
demonstrates how a microlens works. It can also create tiny arcs, but
more commonly the intensity of the lensed object increases over a short
time. Luminosity changed in the point source (like a distant star) can
also be used to determine the strength of the lens. This is done by
comparing brightness levels before and after the lensing event. A simple
method is compare the mass of the actual star, then compare with a mass
of a star of equal brightness of the lensed star – that is, the
increased brightness compared to an actual star of the same brightness.
A second major MACHO
microlensing survey was performed, this time acquiring spectroscopic and
B-V data on more sources – including binary stars. While the equations
and techniques were similar to the first, the benefit of this survey
also allowed for the mass of distant stars (if unknown) to be determined
based on binary and B-V data (Alcock et al., 2000). Again, the primary
lens of this survey is also brown dwarf stars.
Back to Top
| Back to
Cosmology
The Gravity Lens and
Dark Matter – Weak Lensing:
The most common type of
gravitational lensing is that of the weak lens; weak gravitational
lensing results in tangential and radial arcs surrounding and within the
lens. The lens source is usually a galaxy or a cluster of galaxies. The
weak lensing varies greatly from microlensing:
- The mathematics
involved in weak lensing can be a bit too much to swallow for the
scope of this paper, so will not be included
- The Einstein Radius
equation and its variation are not used in weak lensing
- Direct mass
measurements of individual objects are not possible
The weak gravitational
lensing is used instead to map the overall distribution of dark matter
within the halo of galaxies, or within the spaces between galaxies in a
galaxy cluster. The probability of arcs present in any given galaxy or
galaxy cluster helps to determine the overall mass of dark matter within
the lens as well as constrain the mass density of the Universe (Cooray,
1999).

Figure 7: A beautiful example of weak lensing.
By using a variety of
computer simulations and know CDM variables, it is suggested that
lensing of quasars by nearby dark matter filled halos and statistically
evaluating the size and number of arcs created by the halo of the quasar
will constrain the mass density of the Universe (Li and Ostriker, 2002)
which is a recurrent theme of weak gravitational lensing and dark
matter.
To take this a step
further, it is also proposed that the variations in count of radial and
tangential arcs will provide a more accurate distribution of dark matter
(Oguri et al., 2001).
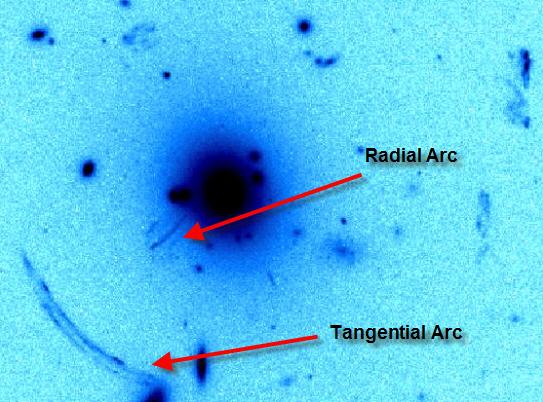
Figure 8.
The image above shows the
difference between a radial arc and a tangential arc. The problem is
that determining the mass profile of dark matter in a halo using these
methods relies on variations of N-Body simulations and comparisons to
current CDM theories. However the first observational test for these
models came in the form of comparing these test situations with
observation data from the Jodrell-Bank VLA Astrometric Survey and the
Cosmic Lens All-Sky Survey (Zhang, 2004). The observed data was in good
agreement with the proposed simulations. The result is a Universe with a
mass density of:
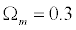 . .
Other observational tests
include study of dark matter halos using surveys like the Suprime-Cam 2
Square Degree Field (Miyazaki et al., 2002).
With the current
observation fitting theoretical models, study of dark matter using weak
gravitational lensing is most effective at studying dark matter directly
(Waerbeke et al., 2002).
By studying weak lensing
in a variety of galaxies with ellipticities (elliptical galaxies
included) between 0.5 and 3.5, the distribution of dark matter has been
shown by observations from the Canada-France-Hawaii Telescope (CFHT) to
be correlated (Waerbeke et al., 2002). This helps to solidify our
current value of the mass density of the Universe.
So what does all this
mean exactly?
The studying of weak
gravitational lensing has:
- Provided valuable
data to determine the mass density of the Universe
- Proved that dark
matter is real
- Dark matter resides
in the halos of galaxies, and is distribution is determined by the
number of arcs present in the lens
- Dark matter also
resides within galaxy clusters and its distribution is also
determined by the number of arcs present
- Elliptical galaxies
also contain dark matter
While weak gravitational
lensing observations and simulations are valuable for cosmology, it
still does not answer the question of what are the constituents of dark
matter.
Back to Top
| Back to
Cosmology
The Gravity Lens and
Dark Matter – Strong Lensing:
Much of the attention in
gravitational lensing has been centered on microlensing and weak lensing,
but there have been some use of the strong lens in helping to solve the
dark matter mystery. By evaluating the strong lensing phenomenon,
astronomers can look to the early Universe dominated mostly by quasars.
The Cold Dark Matter (CDM) model relies on the gravitational lens data
from quasars and the computer models demonstrate that distortions of
arcs from distant quasars as well as secondary reflections will help
correlate the redshift of a quasar (Matsubara, 2000). Such a correlation
was found when the four lensed image (the Einstein Cross) of a quasar
was evaluated for statistical variations in the broad-line and
narrow-line (BLR, NLR) data; however, these statistical analysis is used
primarily for tweaking the CDM model to determine when the galaxy
substructure in the early Universe occurred (Metcalf et al., 2004). This
correlation of redshift and lensing strength was found just recently so
further surveys are needed to collect this valuable data.
Back to Top
| Back to
Cosmology
Summary:
Since dark matter is a
major constituent of matter in the Universe, the detection and measure
of dark matter using lensing techniques has proved vital in determining
the overall density parameter of our Universe. Such implications can
reach deep into the field of cosmology as the density parameter also
determines the value of the Hubble constant as well as the overall shape
of our Universe.
Based on what has been
measure by gravitational lensing, the mass density of the Universe has
been established at:
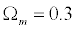
(Li and Ostriker, 2002)(Miyazaki et al., 2002)(Waerbeke et al., 2002).
In addition, the mass
density of the Universe has been constrained to:
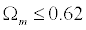
(Cooray, 1999)
which means if the value
of mass density changes, it should not be higher than 0.62. This does
not take into account the contribution of dark energy, which is not
covered here.
The future of
gravitational lensing will require additional direct detection of dark
matter. One proposed project is the detection of massive compact objects
in other galaxies (called MASCO’s). By using yet another variation of
the Einstein Radius equation, it is believed that a survey using optical
and radio (VLBI) maps of other galactic halo that the distribution of
these compact objects will determine the nature of these objects (Inoue
and Chiba, 2003). Such a survey could add valuable data to the Cold Dark
Matter (CDM) model. Up to date data on the current MACHO projects can be
found on The MACHO Project website:
http://wwwmacho.anu.edu.au/. Project OGLE (Optical Gravitational
Lensing Experiment) is an ongoing project to collect real-time data on
MACHO’s near our own galactic center:
http://bulge.astro.princeton.edu/~ogle/.
While many of these
projects are either ongoing or proposed, there is no clear answer as to
what dark matter really is; but gravitational lensing is providing most
of the much needed valuable data to help solve this puzzle.
Back to Top
| Back to
Cosmology
References:
Alcock, C. et al.
“Real-Time Detection and Multisite Observations of Gravitational
Microlensing.” The Astrophysical Journal, 463:L67-L70, June 1, 1996.
Alcock, C. et al. “Binary
Microlensing Events from the Macho Project.” The Astrophysical Journal,
541:270-297, September 20, 2000.
Cooray, Asantha. “An
Upper Limit on Ωm Using Lensed Arcs.” The Astrophysical
Journal, 524:504-509, October 20, 1999.
Inoue, Kaiki Taro and
Masashi Chiba. “Direct Mapping of Massive Compact Objects in
Extragalactic Dark Halos.” The Astrophysical Journal, 591:L83-L86, July
10, 2003.
Li, Li-Xin and Jeremiah
Ostriker. “Semianalytical Models for Lensing by Dark Halos. I. Splitting
Angles.” The Astrophysical Journal, 566:652-666, February 20, 2002.
Matsubara, Takahiko. “The
Gravitational Lensing in Redshift-Space Correlation Functions of
Galaxies and Quasars.” The Astrophysical Journal, 537:L77-L80, July 10,
2000.
Metcalf, R. Benton and
Joseph Silk. “A Fundamental Test of the Nature of Dark Matter.” The
Astrophysical Journal, 519:L1-L4, July 1, 1999.
Metcalf, R. Benton, et
al. “Spectroscopic Gravitational Lensing and Limits on the Dark Matter
Substructure in Q2237+0305.” The Astrophysical Journal, 607:43-59, May
20, 2004.
Miyazaki, Satoshi, et al.
“Searching for Dark Matter Halos in the Suprime-Cam 2 Square Degree
Field.” The Astrophysical Journal, 580:L97-L100, December 1, 2002.
Oguri, Masamune; Taruya,
Atsushi and Yasushi Suto. “Probing the Core Structure of Dark Halos with
Tangential and Radial Arc Statistics.” The Astrophysical Journal,
559:572-583, October 1, 2001.
Silk, Joseph. A Short
History of the Universe. Scientific American Library, New York.
1999.
Turner, Edwin and
Masayuki Umemura. “Very Strong Microlensing of Distant Luminous Stars by
Relic Massive Black Holes.” The Astrophysical Journal, 483:603-607, July
10, 1999.
Waerbeke, L. Van, et al.
“Detection of Correlated Galaxy Ellipticities from CFHT Data: First
Evidence for Gravitational Lensing by Large-Scale Structures.” Astronomy
and Astrophysics Pre-Print, April 28, 2002.
Wambsgauss, Joachim. “Gravitational Lensing in Astronomy.” Living
Reviews in Relativity, Internet:
http://relativity.livingreviews.org/Articles/lrr-1998-12/. 2001.
Zhang, Tong-Jie.
“Gravitational Lensing by Dark Matter Halos with Nonuniversal Density
Profiles.” The Astrophysical Journal, 602:L5-L8, February 10, 2004.
Back to Top
| Back to
Cosmology
Websites:
Hubble Press Release:
http://hubblesite.org/newscenter/newsdesk/archive/releases/1990/20/image/a
Gravitational Lensing:
http://astron.berkeley.edu/~jcohn/lens.html
The MACHO Project:
http://wwwmacho.anu.edu.au/
OGLE:
http://bulge.astro.princeton.edu/~ogle/
The Hubble Newsdesk –
Gravitational Lens:
http://hubblesite.org/newscenter/newsdesk/archive/releases/category/exotic/gravitational
lens/
Back to Top
| Back to
Cosmology
Image Credits (in
order of appearance):
Figure 1:
http://astron.berkeley.edu/~jcohn/lens.html
Figure 2:
http://relativity.livingreviews.org/Articles/lrr-1998-12/
Figure 3:
http://www.mpa-garching.mpg.de/Lenses/museum.en/index.html
Figure 4:
http://hubblesite.org/newscenter/newsdesk/archive/releases/1990/20/image/a
Figure 5:
http://hubblesite.org/newscenter/newsdesk/archive/releases/1995/14/image/a
Figure not labeled:
http://www.llnl.gov/str/June03/Cook.html
Figure 7:
http://hubblesite.org/newscenter/newsdesk/archive/releases/2001/32/image/b
Figure 8:
http://www2.iap.fr/LaboEtActivites/ThemesRecherche/Lentilles/arcs/ms2137.html
Back to Top |
Back to Cosmology |

